最近脑坛可热闹啦,尤其是一帮女生,包括康MM, 可活跃啦。男生多努力哟。
94 兄倡议的这个活动,我非常赞成。 我也想写一些小文章,比如我想写一个《中国古代数学的美丽与哀愁》,可惜题目太大,我最近没有时间更没有能力来写。这里我就偷个懒, 介绍一下勾股数。
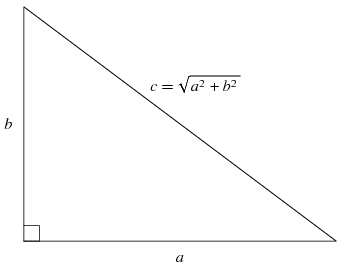
勾股数(组), 西方叫做毕达格拉斯(Pythagoras)数, 是指能够作为直角三角形三边长的三个自然数 x, y, z。 依据勾股定理(或者叫毕达格拉斯定理),如果z是斜边边长,那么 x2+y2=z2. 因为 x, y, z 要求是整数, 要找到很多勾股数曾经并不容易。 在古代,东西方都有人找到一些特例,或者特别的公式. 比如我们先人很自豪的(3,4,5), 传说是商朝时代的商高发现的(他当然也发现了勾股定理)。毕达格拉斯给出了一些特殊公式,刻意求出部分勾股数。巴比伦人更厉害,他们在毕达格拉斯和商高之前千多年,发现了15组勾股数, 由于这些数相当大, 我们有理由相信巴比伦人也有奇妙的公式。这些数都被可在泥板上, 墓碑上,或是金字塔上。总之,在古代发现勾股数可是很重大的成就,不是今天一块奥运金牌能相比的。勾股定理,勾股数与数学发展的关系之深,不是我所能阐发的,打住。--刚才 google 了一下, 发现今天还有中国人宣称发现了奇妙的勾股数公式,可惜我没有兴趣看了。
能求出所有勾股数的公式, 今天看来已经很简单了。每一组勾股数都可以写成下面的形式:
x=k(2ab), y=k(a2-b2), z=k(a2+b2).
其中所有数都是自然数, a > b ( 注意 x 和 y 出于对称位置) . 初中学生都能验证这些 x2+y2=z2. 反过来,要证明对任意一组勾股数(x,y,z), 都能找到 自然数 k, a, b 使得上式成立就难一些了, 但其实也只涉及整除,同余理论之类。
有了这个公式,人类可以说对勾股数相当了解了。涉及勾股数的题目, 有时候不需要这个公式,有时候用了会简单一些。通常要解决这类题目还要用到其他的数论知识,比如整除,同余之类。 用上面这个公式的时候,通常假定 a 与 b 互素,把因子提到 k 那里。 如果 k 也等于 1, 那么 (x,y,z) 三个数都是互素的,称之为原始勾股数。
我们来看一个康MM的一个题目
直角三角形
有一个整数边直角三角形,斜边长是一个二位数,这个数两个数字颠倒过来是一条直角边的边长。斜边长是多少?(不许用computer算)
丑女郎给出了一个相当漂亮的解。这个题目不需要那个公式。
然后haha2000 问了下面这个问题:
哈哈的题
存在一个两位自然数ab, 使得cd 和 dc 是一个所有边长为自然数的直角三角形的两直边之长吗?
我的答案是: 令x=cd=k(2ab), y=dc=k(a2-b2), a 和 b 互素。 那么 cd-dc=9(c-d)=x-y=k((a+b)2-2a2), 由于 a 和 b 互素, 可以验证 3 与 ((a+b)2-2a2, 9 必然整除 k, 也就是说 x 和 y 都是 9 的倍数。剩下的就是试验了,答案是不存在。
问题:
(1), 找出 不超过 50 的不能出现在任何勾股数中的正整数。
譬如 1, 2。 7 不能做 z, 但 7 可以做 y, 即出现在 (24, 7, 25) 中,所以 7 不是一个答案。
2, 如果 (x, y, z) 是勾股数, 那么 60 整除 xyz.
本来刚才还想到一些题目, 写写就忘了。