(一)混沌是什么?
混沌是一种神秘的现实。它似乎意味着一种完全无序的状态,意味着天地未开时的朦胧,更述说着宇宙诞生时的空虚。混沌,就是混乱和无序的代名词。古往今来,无数人尝试走入混沌的世界,却没有人能找到返程的大门,更没有人能寻觅到混沌的精髓。

(图片来源:视觉中国)
对混沌本质的认识,从远古时代对命运的敬畏,伴随着科学史上一次又一次匪夷所思的发现,终于在1963年振翅一飞,破茧成蝶,以“蝴蝶效应”的美名与混沌翩翩起舞。
混沌理论的诞生,更是被誉为20世纪仅次于广义相对论和量子力学的第三大自然科学的发现。从此以后,人们终于触及世界深处的本质。基于对蝴蝶效应的研究,分形理论、混沌理论和非线性动力系统等等复杂理论应运而生。这些理论终于能够解释让世界得以运转的更深层次的规律,终于能够为无常的命运把脉,甚至能够逐步解开生命的密码。
蝴蝶效应告诉人们:巴西热带雨林中的蝴蝶煽动几下翅膀,可能在美国德克萨斯州引起一场龙卷风。这种效应在今天比比皆是。
一些微不足道的小改变,可能会酿成生活的大灾难。一个私密的谣言,可能会让当事人名誉扫地,而受害人却要花费远超过造谣人的成本来弥补这些伤害。一些关于股票的内部消息,可能会引起投资人的恐慌,促使股市灾难性地下跌。历史上,银行发生的挤兑、对生活物资的疯抢、一家私人银行的倒闭引发的金融海啸,都源于一点点信心的丧失。
然而,蝴蝶效应也有好的一面。如果能借力打力,更是可以形成四两拨千斤的神奇效果。互联网时代,通过网络的放大效应,草根阶层也有了逆袭成为明星的机会。一部小成本的电影,如果得到少数精英的推荐,也能引爆市场,成为经典。投资者如果能善用杠杆,用很少的本金就能撬动大笔的资金创造出惊人的财富。
归根结底,正如蝴蝶效应所揭示的那样,初始条件的细微改变会引起事件结果的剧烈波动。一个复杂系统,从诞生起就注定与蝴蝶效应为伴。蝴蝶效应更剑指混沌的特征:在确定性系统中看似随机的无规律行为;由于确定性的规律,短期内可预测;又因为蝴蝶效应的不可预测性,长期则无法预测。
也因为如此,人们的命运变得扑朔迷离。一些小事都可以在我们的生活中引起巨大的不同,甚至会影响国家的命运。有人曾经不恰当地感叹道:如果维也纳艺术学院当初没有再三拒绝希特勒的申请,世界上是否会减少几千万冤死的亡灵。
虽然混沌的表象十分模糊,但它的内心却异常的温柔舒缓。如果把混沌的信号通过扬声器播放,它听上去就仿佛是帮助失眠者入睡的背景音乐。让我们一起去欣赏这曲迷人的音乐,一起去聆听走进这个牵动着古往今来无数人心弦的故事。它的过去和未来,正在向我们展开胸怀。
(二):分形的奇迹——分数维的曲线
混沌的秘密,不可思议地隐藏在分形的世界里。
分形(fractal),该术语最早是由美国数学家曼德勃罗(Mandelbrot)于1973年提出。

曼德勃罗(1924-2010)(图片来源网络)
在其名著《大自然的分形几何学》中,曼德勃罗开创了分形几何学。分形几何以及与其相关的非线性理论,很快就显示出强大的生命力,其影响迅速遍及科学和社会的每个角落。许多学科中的难题,因为分形的介入而焕然一新。如梦初醒的科学家才发现,原来分形的身影已经在世界上默默存在了数亿年,从地球诞生始就向大自然昭示其深邃的奥秘。

植物的分形(图片来源:网络)
生活中常见的花菜、雷雨过后的闪电、凛冬漫天飞舞的雪花、贝壳身上的螺旋图案,小至各种植物的结构及形态,遍布人体全身纵横交错的血管,大到天空中聚散不定的白云、连绵起伏的群山,它们都或多或少表现出分形的特征。乍看起来杂乱无章的分形,原来是大自然的基本存在形式,无处不在,随处可见。

图片来源:视觉中国
(三):人体竟是分形的杰作?!
分形如此广泛地分布在自然界中,却又与千百年来的智者擦肩而过。它的发现,正式揭开了大自然最迷人和动人的奥义之一。
早在两千多年前的古希腊时代,人们最杰出的成就来自数论与几何,特别是欧几里得几何的建立,更使得几何学成为最严格和易于把握的公理化体系。
几何研究的对象是图形。为了研究不同的几何对象,人们倾向于把它们进行归类。从点、线、面到立体,人们的思维逐渐扩展开来。渐渐地,人们意识到区别几何图形的重要分水岭:维度。直线和曲线是一维的图形,平面则是二维的图形,立体则属于三维的空间。

图片来源:视觉中国
一切都是那么的直观,历史在平静地流淌。直到有一天,一件匪夷所思的事打破了人们对维度的信念。
1890年,意大利数学家皮亚诺(Piano)构造了一种奇怪的曲线,该曲线自身并不相交,但是它却能通过一个正方形内部所有的点。换句话说,这条曲线就是正方形本身,进而应该拥有和正方形一样的面积!这个怪异的结论让当时的数学家大吃一惊,更让数学界感到深切的不安:如此一来,我们拿什么来区分曲线和平面?这条曲线究竟是一维,还是二维?经典的几何在它面前束手无策。这只被放逐出来的怪兽,正式奏响了分形几何研究的序曲。
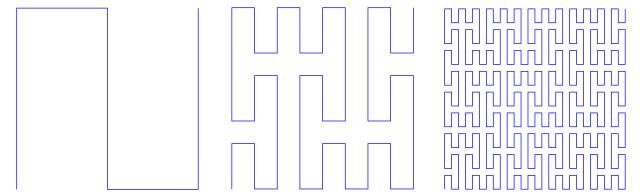
皮亚诺曲线(图片来源:Wikipedia)
维度概念的扩展,则得益于德国数学家豪斯多夫(Hausdorff)。他在1919年提出了维度的新定义。该定义为人们成功驱散了笼罩在分形曲线身上的迷雾奠定了基础。
在传统的观念下,一个空间的维数等于决定空间中任何一点位置所需要变量的数目。比如我们生活的空间之所以是三维空间,源自我们需要三个数值:经度、纬度和高度来确定物体在空间中的位置。这样的定义无比符合人们的直观,也因此在数千年间都被奉为圭臬。但是这种定义维度的方式,排除了分数维的可能。

图片来源:视觉中国
豪斯多夫另辟蹊径,从物体的自相似性来定义维度。自相似性,顾名思义,就是“一个图形的自身可以看成是由许多与自己相似的、大小不一的部分组成的”。比如一条线段是由两个与原线段相似、长度一半的线段接成。一个立方体,则可以看成是由8个大小为自身八分之一的小立方体组成。
简而言之,如果一个图形按照N∶1的比例缩小后。如果原来的图形可以由M个缩小之后的图形拼成的话,这个图形的维数d,就是豪斯多夫维数,定义为 d = ln(M)/ln(N). 在豪斯多夫的定义下,皮亚诺的曲线恰好就是二维!因此它能填满正方形并不奇怪。
皮亚诺曲线就是一条自相似的曲线。它身上揭示了分形的诸多特征:具有自相似性、具有无穷多的层次和细节,可以被无限放大、永远都有结构,最令人惊异的是,它还可以是分数维。比如著名的科赫雪花曲线就是1.26维,谢尔宾斯基三角形则是1.58维。

雪花的分形(图片来源:网络)
皮亚诺曲线发现后的83年,曼德勃罗首次提出了分形几何的概念。他在一次公开演讲中提出了一个看起来让众人乏味的问题:英国海岸线究竟有多长?
人们会轻描淡写地回答:只要用仪器去测量就行啊,只要测量得足够精确,总能得到想要的结果。然而,出乎所有人的意料,如果用不同大小的度量标准来测量海岸线的长度,每次竟然会得出完全不同的结果。当度量标准的尺度越小,测量出来的海岸线的长度会越来越长!随着测量精确的提高,英国海岸线的长度也在迅速趋于无穷!多年以后,科学家们才发现,英国海岸线是一个复杂的分形曲线。根据多次测量所得的结果,英国海岸线的分形维数大约等于1.25。

图片来源:视觉中国
更令众人吃惊的是,英国海岸线里隐藏的秘密竟然也和人体的生命构造息息相关。分形的发现,则将人们引向越来越奇异的科学探索之旅。大自然,处处都彰显出伟大的和谐与统一。
英国的海岸线展示出分形那令人惊异的奇妙性质。海岸线围成的国土面积有限,却拥有近乎无限的长度。然而,更让人意想不到的是,英国的海岸线和人体的构造息息相关。
分形,在上帝创造生命的过程中扮演着至关重要的角色。可以说,没有分形,人类这种伟大而聪慧的生灵可能根本就不会出现。
为了维持人体生存的必需,血管肩负起传递营养的重责。人的身体各处都布满血管,从大动脉到微血管,就是为了保证每个细胞都能从血液的流动中交换必要的成分。大动脉负责主要血液的流动,微血管甚至只能允许单个血细胞通行。考虑到每个细胞都需要直接供血,血液循环系统的总体表面积会非常巨大。然而出乎意料的是,这样一个极为复杂细致、遍布全身的血液网络,其血流量的总体积却仅占据人体体积的5%。
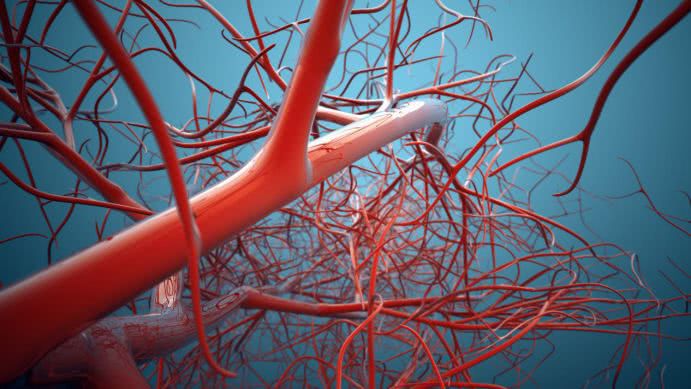
图片来源:视觉中国
科学家经过仔细研究发现:原来,血管的分叉就是一种分形结构。经过精密的实验测定,人体动脉的分形维数大约为2.7。
更进一步,科学家们发现,人体的主要器官和结构都是分形的杰作。
人体的肺部细胞、大脑的表面、肝胆和小肠的结构、泌尿系统、神经元的分布、双螺旋的DNA结构甚至蛋白质的分子链等等,都有明显的分形特征:自相似性。甚至生物体中每个单元的形态结构、遗传特性等,在不同程度上可看作是生物整体的缩影。比如,人耳的形状,就非常类似母体胚胎中蜷缩的婴儿。
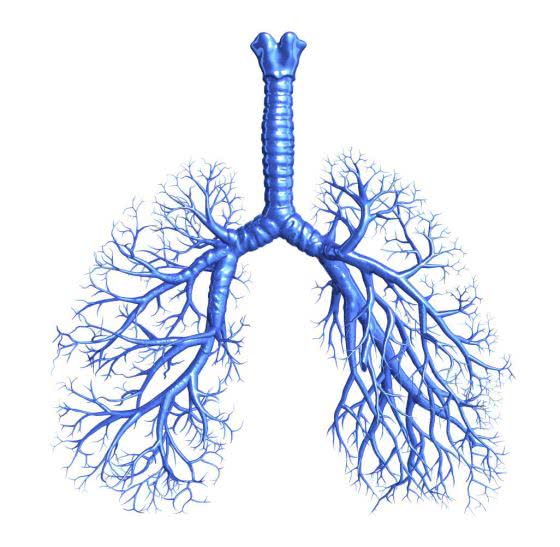
以肺部器官为例。人体的肺部管道,就遵循着反复的树形分叉结构。为了能在有限的体积内充分吸收空气,肺部的表面积竟然差不多和整个网球场一样大,这无疑不是仰赖于分形的功劳!实验揭示,肺泡的分形维数大约为2.97。
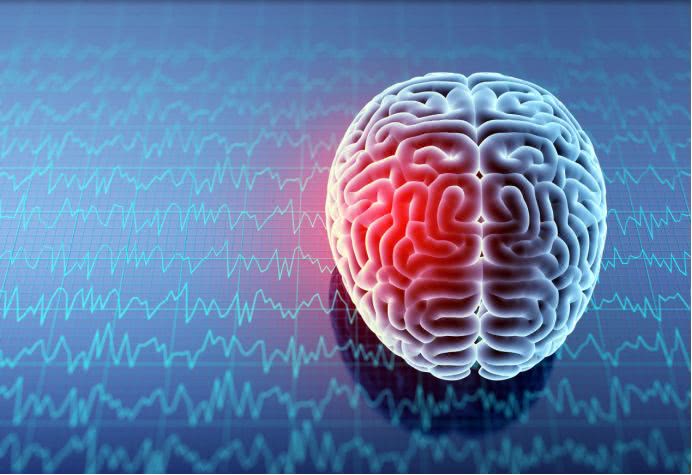
人类的大脑更是分形艺术的杰作。大脑表面的皱纹也呈现出复杂的分形结构,目的就是为了在有限的体积内,能拥有更大的表面积,从而可能拥有更加复杂的思考能力。科学家估算出大脑的分形维数大致在2.75左右。
生命的传承主要依靠细胞的繁殖分裂。单个细胞所蕴含的生物的个体信息,能够全部用于自我复制和重组,成长为一个全新的生命体,这就类似于分形的自相似性。整体的宏观表象,就是每一个细胞的分形合作。
在人体中,除了各种大小器官等的空间分形结构之外,心脏中输送的电流脉冲、心跳节律、脑电波等,这些随时间变动的波形曲线也是分形。不仅如此,人们逐渐认识到,分形甚至是混沌的一种表征结构。事实上,表面上看起来杂乱无章的混沌在某种程度上就可以视为时间上的分形。一个系统的混沌运动是它的本质,分形是它的表现形式;换句话说,混沌学与分形学具有很深的内在联系,如果说分形几何为描写混沌的内部结构提供了一个很实用的语言,那么,混沌运动则被认为是产生分形结构的根源。
分形还有更令人匪夷所思的功能。它除了是人体构成的深层次结构,更能提供人们健康生活的保障。普通人的心脏每分钟都在按照一定频率有规律的跳动。人们想当然地认为心率正常就是身体健康的标志。然而通过对人群的持续追踪则表明:健康人的心率曲线呈现凹凸不平的特征,既有混沌的跳动,又具有分形的自相似性。颠覆人们想法的是,癫痫患者和帕金森病患者的心率曲线反而表现出更多的规则和周期的规律性行为。
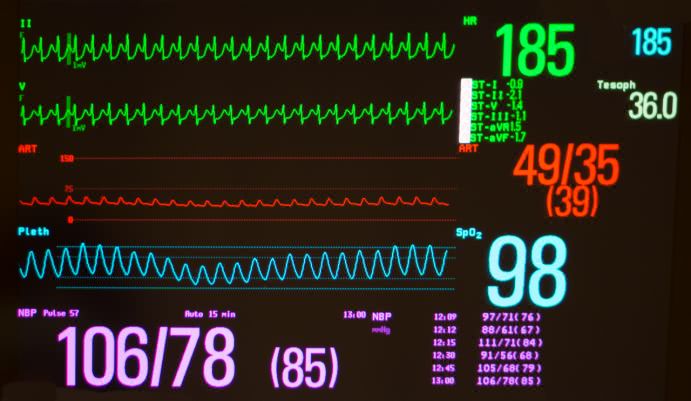
所有的一切都在突破人们对生命系统的传统认知,原来健康的生理特征本质上应该是混沌的。那些在生理上看起来规律的信号,反而可能预示着生命体的异常。
如果考虑到人体的诸多器官和组织都是分形的结构,那么这样的结果也许并不出乎意外。这些器官正常工作产生的信号理应是混沌的。混沌的复杂性、摇摆性,在不同状态随时切换的可能性,才使得人体具有高度的适应性和灵活性,可以去应付外界各种复杂的环境变化。混沌,表面上看起来无迹可寻,却在帮助人体在环境的剧变下生存下来。正如人的大脑也是混沌系统一样,各种微小的外界输入和刺激都能帮助大脑做出天壤之别的反应,这也许正是人类创造性的来源。也正因为混沌的不可预测性,人的行为才有可能表现出智慧和反复的一面。
分形,以及由此产生的混沌,使人类拥有高度的自我进化和调节能力,而一个拥有开放心态和适应能力的生命体,必将能创造更加辉煌的未来。
(四):分形是天使,混沌是魔鬼?
一旦意识到分形的重大意义,人们才发现,分形在世界上无处不在。
近在眼前的人体,其自身的各种器官就有相应的分形结构。远在天边的浮云,则在一个较大的尺度范围内有维数为1.35的边界。英国的海岸线是1.25维的分形,而众多山川地形的表面更是2.2维的分形曲面。

图片来源:视觉中国
分形理论大大打开了各学科的眼界,逐渐渗透到物理、化学、地质、地理、生物、医学、冶金等科学领域。科学家们则从这门新兴的分形理论中获得许多前所未有的新认识和新进展:物理中的湍流与相变,化学中的高分子链、催化剂表面、凝胶,天文学中的星团分布、宇宙大尺度结构,地学中的渗流、地貌演化,地理中的河流与水系,医学中的人体组织结构,材料的损伤断裂等等。
不仅在自然科学领域大放异彩,分形更是在经济学和人文科学的领域里攻城伐地。经济学家用混沌理论预测经济的未来和股市的走势。在人类社会活动和社会现象中,很多地方都呈现出自相似性,这就是社会分形。作家用一部微缩作品反映一个时代的变迁就是一个社会分形元,比如曹雪芹的《红楼梦》描述了晚清时期的社会分形。

图片来源:百度百科
从数学上来看,分形大多数是用非线性迭代法产生的。分形几何的创始人曼德勃罗曾经留下了迄今为止最奇异、魔幻的几何图形--曼德勃罗集。曼德勃罗集被称为“上帝的指纹”和“魔鬼的聚合物”。它就是由简单的非线性迭代所描述: Z(n+1)=Z(n)^2+C,这里Z和C都是复数。

曼德勃罗集(图片来源:百度百科)
由曼德勃罗集出发,分形也为艺术家提供了大量的灵感。基于分形的原理,各种别出心裁的建筑设计更是层出不穷。分形几何理论的建立深深地影响了建筑学的发展,拓展了建筑形式的可能性。不仅如此,分形也深入到音乐和绘画中的创作中,极大地丰富了人们的审美空间。
分形,俨然是宇宙中的天使,为万物奠定秩序和生机;而混沌,犹如黑暗中的魔鬼,为世界带来混乱和挑战。是什么力量,让世界在永恒的时间里同时趋于混乱和秩序?是什么力量,让魔鬼和天使和谐地相处在一起?原来,混沌呈现出的无规行为或无秩序,只是一种表面现象,只有深入到它的内心,才能发现其深刻的规律性。

图片来源:视觉中国
混沌一词在中文里最早出现于盘古开天劈地的传说之中,在《圣经》中也是指代天地初开时的空虚模糊。
西方世界自牛顿创立三大定律一来,一度相信世界的本质是确定性的结果。这种机械宇宙论发展到极致,更是被数学家拉普拉斯高傲地宣称:只要知道宇宙某一刻全部物质的状态,我们就能完全知晓宇宙的过去和未来。然而,牛顿的理论虽然取得巨大的成功,但是仍然在计算太阳系所有行星的运动时无能为力,甚至在预测太阳、地球和月亮的命运时都遭遇到巨大的理论挫折。这个困扰牛顿的难题,也被后世称为三体问题而声名大噪。
法国大数学家庞加莱曾经为三体问题殚精竭虑。即使对问题做出极大的简化,三体问题仍然复杂得让人望而生畏。他曾经失望地表达三体问题的计算难度远远超过想象。人们如此关心三体问题的结局,一方面是出于挑战难题的兴趣,另一方面也是对人类自身命运的关怀。如果牛顿理论是确定无疑的,那么三体问题的解答将给出人类所处的这个星球最后的命运归属。

庞加莱(图片来源:百度图片)
尽管庞加莱未能解决三体问题,但是他却意外地发现一个惊人的事实:太阳系长期的轨道行为是不可预测的!初始条件非常小的变化,会导致之后的运动产生巨大的改变。
1963年,美国气象学家洛伦兹也发现了类似的现象。洛伦兹在用计算机求解一个简化的大气对流模型时,发现这些解以不规则、甚至是随机的方式震荡。初值的极小波动会引起解的剧烈变化。这种奇异的现象后来成了人们耳熟能详的描述:一只巴西热带雨林中的蝴蝶煽动几下翅膀,可能在美国德克萨斯州引起一场龙卷风。这就是大名鼎鼎的“蝴蝶效应”。
洛伦茨用三个变量、三个方程描述了系统的运动,用三维空间来画出三变量系统的轨迹。点的轨迹永远不相交,它永远地在打圈子,表现出一种无穷尽的复杂性。图像一直保持在一定的范围内,既不重复自己,又不跑到纸外。轨迹形成了一个奇怪而明确的图案,像三维空间的一对旋涡,又像一对蝴蝶的翅膀。这就是为后人津津乐道的“蝴蝶吸引子”。

图片来源:百度百科
蝴蝶吸引子是非线性动力系统的神奇现象之一,然而科学家一直没有找到适当命名这一大类问题的方法。1975年,华人科学家李天岩和其博士生导师约克才在其论文中为这种离散动力系统所呈现出的奇异特性命名为“混沌”。自此,混沌终于现身,它打开了现代动力系统研究的大门。科学家终于凌厉地突破自牛顿时代以来一直统治着科学的线性的、还原论的思维方式。
正是混沌魔鬼的现身,让长期的天气预报成为不可能。在现实生活中,天气的实际测量总是存在误差,然而哪怕在小数点后面100位的数字变动了一点,天气预报的结果都可能会大相径庭。太阳系也存在类似的问题,这也让预测人类的终极命运成为永恒的未知。事实上,人们最多只能预测太阳系未来1000年的动力学行为。

图片来源: 视觉中国
非线性系统,由于混沌造成了无法跨越的困难,也因此,混沌被视为自然科学中的魔鬼,阻扰着人们对真理的终极认知。
奇妙的是,混沌的魔鬼只是披着表面的任性,它的内心同样遵循着秩序。美妙的蝴蝶吸引子,提供了混沌从无序迈向有序的铁证。它是链接混沌和分形的桥梁。吸引子实际上是一个具有无穷结构的分形。数学家发现洛伦茨吸引子的分形维数,在2.06左右。
天使和魔鬼,原本就是一家人。
(五):未来,一切皆有可能
混沌的表面模糊不清,然而其核心却和分形紧密联系在一起。
无论是洛伦兹气象模型还是三体问题,都是一个确定性的微分方程,最终却产生了混沌的现象。混沌是系统长期演化的结果。因此,研究一个动力学系统的长期行为才有可能揭示混沌的本质。原来,一个系统的状态会随着某些参数的变化从平衡走向混沌。这个事实被称为倍周期分岔现象。
当参数的取值在一定范围时,系统会长期趋于一个稳定的状态。这个状态就是人们期望预知的终极状态。比如一个在空气中运动的小球如果没有其他外力的驱使,最终会静止下来。这种静止态就是小球的归宿。可是当参数的取值发生变化时,系统的终极状态不再是唯一的,而可能是在两个状态之间彼此摇摆。系统在单位时间内从一个状态跳到另外一个状态,然后再次经历单位时间,系统再次从另外一个状态跳回来。因此,系统回到相同状态的时间就变成了单个状态的两倍。随着参数值的继续增加,终极状态的数目也在迅速增加,每次都会以两倍的形式递增。这就是倍周期分岔现象。
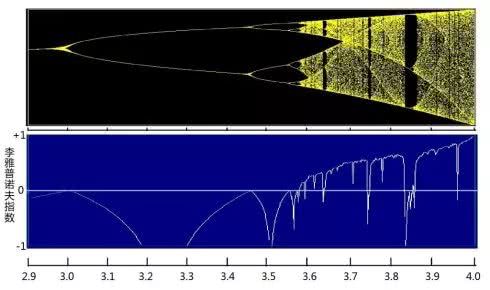
倍周期分岔(图片来源: 网络)
倍周期分岔现象是系统出现混沌的先兆,最终会导致有序到无序,稳态向混沌的转变。当参数出现更大的变化时,倍周期分岔现象呈崩溃之势,平衡点已无法区分,连接成一片连续区域。此时就出现了混沌。而倍周期分岔现象就具有自相似性及普适性等重要的特征。这个与内在随机性密切相关的几何性质揭示了倍周期分岔现象与分形、混沌、奇异吸引子等之间的内在联系,也成为混沌内蕴的秩序象征。
凡事皆有利有弊。混沌的出现带来了混乱,却也在某方面带来了希望。既然扰动会带来破坏性的结果,那么寻找合适的小扰动,就可以起到四两拨千斤的效果。这就是混沌控制的精髓。
太空旅行中,也许通过混沌控制,使用极少的燃料就能实现星际穿梭。混沌里的蝴蝶效应更可以在医学上一展宏图,诸如控制心律失常、抑制癫痫等等,甚至还能让湍流过渡为平稳的运动,减少飞机的危险。

图片来源: 视觉中国
不仅如此,混沌甚至是调节国民经济、缓冲经济危机的利器。众所周知,股市是经济的晴雨表。传统经济学认为,股市是随机游走的布朗运动,其波动符合对数正态分布。由于其高度的随机性,人们无法预测股市的未来,更无法指定合适的政策来维护股市的稳定。
然而,经过多年的实际观测,股市的表现更多呈现出尖峰肥尾的特征,在一定程度上偏离了随机游走的假设。1982年,美国经济学家德依引入了混沌研究经济学的表现。随后,人们开始在各种市场上应用混沌理论寻找其吸引子的特征,并取得非凡的结果。经济呈现出的混沌现象愈来愈多。
经济混沌的存在,虽然不能极大改进经济预测的能力,但是却可以大幅度改善政府对市场的调控能力。这对经济周期的波动和股市的灾难预警提供了更多的宏观政策依据。

图片来源: 视觉中国
混沌的极端不稳定性和对初值的敏感依赖还被用于通信加密。信号一旦被监听干扰就会产生不可逆转的误差,这为破译信号带来极大的的困难,更是开辟了通信技术的新天地。
分形是天使,它呈现出的玄机和美感为人类提供了丰富的灵感源泉。美妙的分形奏响了一曲迷人的音乐篇章,其深刻的本质完全颠覆了人们对传统事物的认识。
混沌是魔鬼,它成为复杂现象的代名词,更是牛顿的确定科学论终结的标志之一。混沌为人们探索真理的疆域划定了边界。在混沌的笼罩下,人们无法预知诸多复杂系统的未来。然而,这也激发了人类持续进步、永不枯竭的创造能力。世界的命运就掌握在你我手中,没有什么比确定性的结局更让人沮丧,也没有什么比一切皆有可能更加振奋人心。
天使和魔鬼,组成了世界运行的规则。它就是真实世界的两面。在魔鬼的内心,隐藏着天使的灵魂。在天使的背后,潜伏着魔鬼的骚动。认识世界的复杂性,摒弃单一的二元对立思维,才能真正走入现代科学的复杂时代,迎接更多可能的未来。
参考文献:
1.《数学的故事》,伊恩.斯图尔特著,上海辞书出版社,2013。
2.《从混沌到有序人与自然的新对话》,伊里亚·普里戈金、斯唐热著,上海译文出版社,1987。
3.《复杂》,米歇尔.沃尔德罗普著,生活·读书·新知三联书店,1997。
4.《蝴蝶效应之谜》,张天蓉著,清华大学出版社,2013。