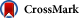Cell: 数学建模癌症化疗给药
|
Improving Cancer Treatment via Mathematical Modeling: Surmounting the Challenges Is Worth the Effort
Drug delivery schedules are key factors in the efficacy of cancer therapies, and mathematical modeling of population dynamics and treatment responses can be applied to identify better drug administration regimes as well as provide mechanistic insights. To capitalize on the promise of this approach, the cancer field must meet the challenges of moving this type of work into clinics.
给药时间安排是癌症治疗效率的重要因子。对群体动态和治疗反应数学建模,能被用来找到更好地给药安排,也能提供更深入地机制。要采用这一有前景的方法,癌症领域必会面临把这一工作转化到临床的挑战。
Figure 1
Exploring Complex Dependencies in Cancer Biology with Mathematical Modeling
The complexity of cancer includes not only the heterogeneous cell population of a tumor, but also its interaction with the microenvironment and immune system and responses to different kinds of treatments. Mathematical modeling of the impact of these factors on tumor cell population dynamics facilitates the generation testable hypotheses regarding the evolution of resistance and identifying prospectively optimum treatment strategies designed to maximize the chance of a cure.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Cancer research and oncology has entered a new era of targeted therapy (Sawyers, 2004Sawyers, 2004) and patient-tailored therapeutic intervention (Shrager and Tenenbaum, 2014Shrager and Tenenbaum, 2014), but resistance (Gottesman et al., 2002, Holohan et al., 2013) and tumor heterogeneity (Anderson et al., 2011, Burrell et al., 2013, Ding et al., 2012, Gerlinger et al., 2012, Landau et al., 2013) have been a barrier for realizing the clinical impact of these discoveries. This barrier is, in essence, a quantitative population genetics problem—the need to quantitatively describe heterogeneous tumor cell populations and their dynamics over time and during treatment. Using such mathematical descriptions, it is then possible to evaluate which drugs, combinations, and schedules are best for a given patient. For instance, if drugs are administered at sufficiently low doses, no drug holidays are necessary to limit the side effects and reduce patient toxicity; however, if drugs are administered at more concentrated doses, which may lead to higher cell kill, then rest periods are needed to limit side effects. Such drug holidays can lead to an exponential rebound of the tumor cell population and hence pose a significant risk for the emergence of resistance. It is unclear, a priori, which of these two example strategies are going to be more effective in reducing tumor burden and preventing the emergence or outgrowth of a resistant tumor subclone. In order to answer this question, several clinical studies have been performed to identify optimum dosing frequencies (Hryniuk, 2001, Lake and Hudis, 2004). However, it is both unethical and too time consuming to test all possible dosing schedules in pre-clinical or clinical studies, and therefore only limited clinical experimentation can be performed.
Mathematical modeling of the treatment response of heterogeneous cell populations represents an attractive avenue toward narrowing the set of possibilities that should be tested in pre-clinical models and in the clinical setting (Figure 1Figure 1). Mathematical modeling can, in principle, be used to systematically search through the millions of possible dose administration strategies (each determined by a unique dose-time profile) and combination schedules (each determined by a combination of different drugs administered at different dose-time profiles) to identify the schedules that maximally extend patient survival. Indeed, a significant amount of research effort has been devoted to developing mathematical models that identify the most effective chemotherapeutic administration regimens using optimization and control techniques (Coldman and Murray, 2000, Costa et al., 1992, Costa et al., 1995, Katouli and Komarova, 2011, Kimmel and Swierniak, 2006, Ledzewicz and Schattler, 2009, Martin et al., 1992, Martin and Teo, 1993, Murray and Coldman, 2003). These models are in general aimed at rapidly minimizing the total tumor burden. However, long-term patient survival depends not only on quickly decimating the total number of tumor cells, but also on controlling drug-resistant subpopulations within the tumor. The simultaneous achievement of these two goals is complicated by the fact that they are often accomplished by exerting opposing evolutionary selection pressures. Furthermore, both long-term toxicity and dose-limiting side effects must be avoided.
Figure 1
Exploring Complex Dependencies in Cancer Biology with Mathematical Modeling
The complexity of cancer includes not only the heterogeneous cell population of a tumor, but also its interaction with the microenvironment and immune system and responses to different kinds of treatments. Mathematical modeling of the impact of these factors on tumor cell population dynamics facilitates the generation testable hypotheses regarding the evolution of resistance and identifying prospectively optimum treatment strategies designed to maximize the chance of a cure.
Below, we will highlight several examples of promising, modeling-based findings, some of which represent the few that have been or will soon be tested clinically. We will then discuss the challenges that the field must meet to enable more extensive clinical testing of mathematically discovered treatment modalities. In a landmark study, Norton and Simon (Norton and Simon, 1977Norton and Simon, 1977) observed that clinical experience was at odds with a fundamental concept that had been instrumental in designing dose schedules for the treatment of human cancer: that small tumors were more sensitive to cytotoxic therapy than larger tumors of the same histology. The underlying assumption was that smaller tumors have a large fraction of actively dividing cells. However, Norton and Simon observed that, in many cases, the low-dose low-concentration schedules used for smaller tumors were inferior to more high-concentration, dose-dense protocols that were a relatively novel approach at that time. To understand this observation, they probed the relationship between tumor size and sensitivity to therapy by inspecting growth curves of tumors exposed to anti-cancer agents. They found that most untreated malignancies can be described using a Gompertzian growth law, which predicts an S-shaped growth curve. According to this law, the growth rate of tumor cells is smallest for both very small and very large tumors but is maximum at the inflection point. Their resulting mathematical model led to the conclusion that a dose schedule capable of dramatically depleting a tumor of intermediate size may not be sufficient to cure a small tumor. They thus suggested more intense schedules, higher doses, and prolonged therapy. The authors later set out to validate their predictions in a large randomized clinical trial (Citron et al., 2003Citron et al., 2003) of axillary node-positive breast cancer. They found, as predicted, that dose-dense schedules significantly increased disease-free survival and overall survival. Their approach thus became the first mathematical model providing clinically validated predictions.
The model by Norton and Simon was based on the observation that treatment efficacy can drop if insufficient drug is administered at a time when the tumor is kinetically less sensitive to treatment. This “kinetic resistance” is unlike acquired resistance due to genetic and/or epigenetic events that prevent the drug from entering the cell, binding to its target, or other mechanisms. This “biochemical” type of resistance was first mathematically addressed by Goldie and Colman, who developed a mathematical model relating the probability of drug sensitivity of a tumor to the rate at which cells accumulate changes that enable them to become resistant to therapy (Goldie and Coldman, 1979Goldie and Coldman, 1979). The model assumed that there is a certain probability per cancer cell division that a resistance-causing (epi)genetic change arises. By calculating the probability of resistance and the expected number of resistant cells, the authors found not only that an increase in the mutation rate increases the probability of a resistant phenotype emerging, but also that the probability of there being at least one resistant cell will increase dramatically during a very short interval in the biological history of the tumor. The clinical recommendation based on these results was that therapy be initiated as quickly as possible to maximize the probability of a cure. This approach was later also predicted to maximize patient survival due to the emergence of more lethal cancer states such as metastases (Haeno et al., 2012Haeno et al., 2012).
A subsequent extension of this mathematical model considered two types of resistant cells, each insensitive to a different chemotherapeutic agent (Goldie et al., 1982Goldie et al., 1982). The goal of the model was to take both types of resistance into account and identify treatment schedules that would maximize the chance of a cure by preventing the emergence of doubly resistant cells. Using a computer program to simulate the development of such doubly resistant cells, the authors predicted that alternating the treatment regimen of the two drugs at every cycle would be the most effective strategy to prevent resistance. This prediction became known as the Goldie-Coldman hypothesis. A clinical trial in Italy tested this hypothesis in women with resectable mammary carcinoma and more than three positive axillary lymph nodes (Bonadonna et al., 1995Bonadonna et al., 1995). The patients were randomized into two treatment arms, either receiving treatments sequentially or in an alternating fashion. The primary endpoints were relapse free, and overall survival and the median duration of follow-up was 9 years. The trial results demonstrated significantly longer survival, both progression free and overall, for patients who received the sequential regimen as compared to the alternating regimen. A subsequent phase II study also evaluated the efficacy of alternating and sequential regimens of docetaxel and doxorubicin as first-line chemotherapy for metastatic breast cancer (Paridaens et al., 2003Paridaens et al., 2003). The alternating and sequential groups achieved similar objective tumor response rates and median duration of response, but medial survival times were significantly shorter in the alternating than the sequential group. Furthermore, patients receiving sequential therapy were more likely to complete the planned eight chemotherapy cycles and had a lower incidence of side effects.
These trial results suggest that, at least in those clinical settings, the Goldie-Coldman hypothesis did not hold. However, the possibility remains that the hypothesis might lead to better survival times in other cancer types and/or treatment approaches (such as chemotherapy and radiation therapy). Indeed, several studies have investigated the outcome of radiation therapy followed by chemotherapy versus chemotherapy concomitant with radiation therapy. For example, in non-metastatic breast cancer, both radiation and chemotherapy are often used as adjuvant treatment following surgery. A randomized study performed in the 1990s comparing the sequencing options (of radiation versus chemotherapy first) showed a reduction in the rate of distant metastases in the group that received chemotherapy first (Recht et al., 1996Recht et al., 1996). However, those results were later updated (Bellon et al., 2005Bellon et al., 2005) and shown to be non-significant and were then disputed in a meta-analysis of three well-documented randomized trials designed to study this question (Hickey et al., 2013Hickey et al., 2013). Thus, the findings regarding implementations of the Goldman-Coldie hypothesis in the clinic remain mixed, and no clear validation of the hypothesis has been obtained so far. In fact, other recent approaches have suggested that it would be beneficial to administer combination treatment upfront to prevent the outgrowth of resistance (Bhang et al., 2015, Bozic et al., 2013, Glickman and Sawyers, 2012).
To determine whether modeling approaches could be applied to specific resistance mechanisms to individual drugs, we developed a mathematical model of non-small cell lung cancer cell response to treatment with the epidermal growth factor receptor (EGFR) inhibitor erlotinib (Chmielecki et al., 2011Chmielecki et al., 2011) in which resistance was considered to arise predominantly due to a second-site EGFR mutation (Pao et al., 2005Pao et al., 2005), T790M, which emerges with a low probability during each sensitive cell division. The model, similar to the approach by Goldie and Coldman, was based on a stochastic branching process in which erlotinib-sensitive cells proliferate and die according to rates determined in a patient-derived cell line. Resistant cells then also proliferate and die according to rates determined in cells isogenic to the sensitive line apart from the T790M mutation. These in vitro cell culture experiments demonstrated that resistant cells had a fitness lower than sensitive cells in the absence of treatment, a finding explaining the low frequencies of pre-existing T790M-positive clones in patients (Chmielecki et al., 2011Chmielecki et al., 2011). The mathematical model was then used to search through the space of all clinically tolerated erlotinib schedules to identify the one that would significantly delay the emergence of T970M-driven resistance. Unlike the FDA-approved schedule of 150 mg per day, the optimum consisted of administering a low dose of 50 mg per day together with twice weekly high-dose pulses at the clinically determined maximally tolerated dose; the clinical study testing this hypothesis was initiated at Memorial Sloan-Kettering in 2013 (http://clinicaltrials.gov/show/NCT01967095). Preliminary results show that this schedule is well tolerated and might reduce the rate of progression in patients with brain metastases (H.A. Yu et al., 2015, ASCO, poster).
Although only these three population-based modeling approaches have so far led to clinical implementation, several other frameworks have been developed that might soon be tested in the clinic. These include a mathematical model suggesting the use of an adaptive therapeutic approach that changes in response to the variability in both space and time of the tumor microenvironment, cell phenotype, and response to treatment (Gatenby et al., 2009Gatenby et al., 2009) and a model investigating alternative radiation schedules in primary glioblastoma (Leder et al., 2014Leder et al., 2014). Another recent approach incorporates genetic heterogeneity in the context of selecting optimum combination strategies (Zhao et al., 2014Zhao et al., 2014). Other groups have used evolutionary game theory to investigate optimal combination therapies (Basanta et al., 2012Basanta et al., 2012) or have used patient-derived data on tumor stem cell turnover to identify prognostic factors (Stiehl et al., 2015Stiehl et al., 2015).
These studies serve as examples of quantitative descriptions of heterogeneous cell populations responding to treatment. The potential of this approach is obvious—it enables us to systematically investigate hypotheses and test alternative options for treatment. While mathematical models and pre-clinical studies of optimized treatment schedules are encouraging, limitations of the approach are also plentiful, as illustrated by the lack of resolution regarding the efficacy of alternating versus sequential treatments discussed above. The predictive utility of a model parameterized using a particular pre-clinical model depends on the accuracy not only of the mathematical model, but also the in vitro or in vivo model vis a vis the human cancer that it models, as well as the biological assumptions and quality of the data. The ability of the modeling predictions to be verified or falsified—not just in a model system, but eventually in a clinical study—is the essential test. In addition, knowledge is evolving: more complex aspects of tumor biology are emerging and need to be incorporated into quantitative modeling approaches. These include single-cell genetic and epigenetic heterogeneity (Van Loo and Voet, 2014Van Loo and Voet, 2014) and interactions between cancer cells and the immune system (Sharma et al., 2011Sharma et al., 2011) as well as the microenvironment. The analysis of datasets that comprehensively and quantitatively capture such features may require novel mathematical approaches and simulation tools that, for instance, can take advantage of today’s most powerful supercomputers.
Importantly, translation of these concepts and ideal models into a clinical setting presents both logistical and patient-specific challenges related to the tumor micro-environment. It is always difficult to translate a result from a cell line or animal model into a human clinical study; while there are logistical concerns related to administering any type of cancer-related treatment, we will discuss the complexities of treating brain tumor patients with radiation as a specific example. The first challenge regarding scheduling altered or “optimized” scheduled radiation, for instance, as proposed in Leder et al. (2014))Leder et al. (2014), reflects the process of treating patients at a specific time each day. There are staffing concerns with respect to hours of operation and coordination of scheduling multiple patients throughout the day on each linear accelerator. There is also the potential of treatment- or tumor-related toxicity that may fluctuate daily and may affect whether or not patients can tolerate treatment at very specific time(s) each day. Most patients are also fatigued and may have neurologic symptoms related to their brain tumors or treatment, which makes it difficult to adhere to a complicated or specific timing schedule. With careful patient selection and consideration of scheduling constraints, though, these challenges may be overcome. The observation of variable tumor volume among patients reflects the fact that there is great variability among patients with the extent of their brain tumor resection related to the location of their tumors in different regions of the brain and the original extent of the tumor. A patient who has a gross total resection with only microscopic residual disease may have a very different response to an altered or optimized treatment schedule than a patient who has a large, relatively intact tumor. The potential variability of tumor volume between brain tumor patients is much greater than in the breast cancer studies referred to above. This variability could certainly affect the outcome of an optimized radiation schedule clinical trial.
Other challenges are related to variability in the tumor microenvironment that may be the result of molecular differences among patients’ tumors or even more simply the wide range of medications, or chemotherapy, that brain tumor patients often require as part of the management of their brain tumors. These medications may alter the cancer cells’ sensitivity to radiation or may change the vascular environment and thus indirectly affect sensitivity to radiation. Even if a study were designed that controlled for the use of common medications for brain tumor patients, such as corticosteroids, antiepileptics, or temozolomide, the requirements of some medications are likely to change during the course of radiation, or patients may discontinue some medications in the midst of their course of radiation due to toxicity. There are innumerable possibilities of drug combinations during radiation therapy for brain tumors that could both positively and negatively impact the effect of radiation. The exact schedule of those standard adjuvant chemotherapies, or perhaps investigational immunotherapies, may also alter the radiosensitivity, or clonal expansion, possibilities at any given moment. A fully optimized model would need to incorporate those possible influences as well.
Despite these challenges in designing and effectively executing a clinical trial to test treatment regimes derived from mathematical modeling and preclinical data, the endeavor should be pursued. The results with the current standard treatment are suboptimal, with a median survival of only 15 months for patients with primary glioblastoma, the most common type of malignant brain tumor. However, following surgery, radiation remains the most effective therapy for glioblastoma, and thus optimizing the effect of radiation remains an attractive option. Historically there have been many studies of various schedules of radiation for glioblastomas, including dose escalation, but the results from all are disappointing to date (Brada et al., 1999, Horiot et al., 1988; W.J. Curran et al., 1996, Proc. Am. Soc. Clin. Oncology, abstract). Notably, none of these studies have been based upon a mathematically optimized schedule. A hypothesis worth testing is that a clinical trial of a mathematically optimized radiation schedule could yield an improved result and could identify altered radiation scheduling as an opportunity for improved outcomes in other types of brain tumors or other cancer types.
Despite the logistical, tumor-, and patient-specific challenges listed above, a trial of an optimized radiation schedule is an achievable goal with careful patient selection, patient management, and support from all of the stakeholders, including clinicians, scientists, and the patients and their families. The glioblastoma mouse model study comparing a standard schedule to an optimized schedule (Leder et al., 2014Leder et al., 2014) proves the concept that an altered radiation schedule can affect survival. This theory must be tested in humans with glioblastoma, as these patients need every opportunity possible to improve their outcome.
Despite the operational, biological, and mathematical obstacles that need to be overcome for successful implementation of a mathematically predicted treatment strategy in the clinic, we strongly believe that surmounting these challenges is worth the effort. The Norton-Simon hypothesis was the first demonstration that a mathematically derived schedule might be clinically superior, but many recent and forthcoming approaches hold great promise, and we have high expectations that rational quantitative investigations might contribute to new hope for cancer patients.
References
Authors
Title
Source
- Anderson et al., 2011Anderson, K., Lutz, C., van Delft, F.W., Bateman, C.M., Guo, Y., Colman, S.M., Kempski, H., Moorman, A.V., Titley, I., Swansbury, J. et al. Genetic variegation of clonal architecture and propagating cells in leukaemia. Nature. 2011; 469: 356–361
- Basanta et al., 2012Basanta, D., Gatenby, R.A., and Anderson, A.R. Exploiting evolution to treat drug resistance: combination therapy and the double bind. Mol. Pharm. 2012; 9: 914–921
- Bellon et al., 2005Bellon, J.R., Come, S.E., Gelman, R.S., Henderson, I.C., Shulman, L.N., Silver, B.J., Harris, J.R., and Recht, A. Sequencing of chemotherapy and radiation therapy in early-stage breast cancer: updated results of a prospective randomized trial. J. Clin. Oncol. 2005; 23: 1934–1940
- Bhang et al., 2015Bhang, H.E., Ruddy, D.A., Krishnamurthy Radhakrishna, V., Caushi, J.X., Zhao, R., Hims, M.M., Singh, A.P., Kao, I., Rakiec, D., Shaw, P. et al. Studying clonal dynamics in response to cancer therapy using high-complexity barcoding. Nat. Med. 2015; 21: 440–448
- Bonadonna et al., 1995Bonadonna, G., Zambetti, M., and Valagussa, P. Sequential or alternating doxorubicin and CMF regimens in breast cancer with more than three positive nodes. Ten-year results. JAMA. 1995; 273: 542–547
- Bozic et al., 2013Bozic, I., Reiter, J.G., Allen, B., Antal, T., Chatterjee, K., Shah, P., Moon, Y.S., Yaqubie, A., Kelly, N., Le, D.T. et al. Evolutionary dynamics of cancer in response to targeted combination therapy. eLife. 2013; 2: e00747
- Brada et al., 1999Brada, M., Sharpe, G., Rajan, B., Britton, J., Wilkins, P.R., Guerrero, D., Hines, F., Traish, D., and Ashley, S. Modifying radical radiotherapy in high grade gliomas; shortening the treatment time through acceleration. Int. J. Radiat. Oncol. Biol. Phys. 1999; 43: 287–292
- Burrell et al., 2013Burrell, R.A., McGranahan, N., Bartek, J., and Swanton, C. The causes and consequences of genetic heterogeneity in cancer evolution. Nature. 2013; 501: 338–345
- Chmielecki et al., 2011Chmielecki, J., Foo, J., Oxnard, G.R., Hutchinson, K., Ohashi, K., Somwar, R., Wang, L., Amato, K.R., Arcila, M., Sos, M.L. et al. Optimization of dosing for EGFR-mutant non-small cell lung cancer with evolutionary cancer modeling. Sci. Transl. Med. 2011; 3: 90ra59
- Citron et al., 2003Citron, M.L., Berry, D.A., Cirrincione, C., Hudis, C., Winer, E.P., Gradishar, W.J., Davidson, N.E., Martino, S., Livingston, R., Ingle, J.N. et al. Randomized trial of dose-dense versus conventionally scheduled and sequential versus concurrent combination chemotherapy as postoperative adjuvant treatment of node-positive primary breast cancer: first report of Intergroup Trial C9741/Cancer and Leukemia Group B Trial 9741. J. Clin. Oncol. 2003; 21: 1431–1439
- Coldman and Murray, 2000Coldman, A.J. and Murray, J.M. Optimal control for a stochastic model of cancer chemotherapy. Math. Biosci. 2000; 168: 187–200
- Costa et al., 1992Costa, M.I., Boldrini, J.L., and Bassanezi, R.C. Optimal chemical control of populations developing drug resistance. IMA J. Math. Appl. Med. Biol. 1992; 9: 215–226
- Costa et al., 1995Costa, M.I., Boldrini, J.L., and Bassanezi, R.C. Drug kinetics and drug resistance in optimal chemotherapy. Math. Biosci. 1995; 125: 191–209
- Ding et al., 2012Ding, L., Ley, T.J., Larson, D.E., Miller, C.A., Koboldt, D.C., Welch, J.S., Ritchey, J.K., Young, M.A., Lamprecht, T., McLellan, M.D. et al. Clonal evolution in relapsed acute myeloid leukaemia revealed by whole-genome sequencing. Nature. 2012; 481: 506–510
- Gatenby et al., 2009Gatenby, R.A., Silva, A.S., Gillies, R.J., and Frieden, B.R. Adaptive therapy. Cancer Res. 2009; 69: 4894–4903
- Gerlinger et al., 2012Gerlinger, M., Rowan, A.J., Horswell, S., Larkin, J., Endesfelder, D., Gronroos, E., Martinez, P., Matthews, N., Stewart, A., Tarpey, P. et al. Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. N. Engl. J. Med. 2012; 366: 883–892
- Glickman and Sawyers, 2012Glickman, M.S. and Sawyers, C.L. Converting cancer therapies into cures: lessons from infectious diseases. Cell. 2012; 148: 1089–1098
- Goldie and Coldman, 1979Goldie, J.H. and Coldman, A.J. A mathematic model for relating the drug sensitivity of tumors to their spontaneous mutation rate. Cancer Treat. Rep. 1979; 63: 1727–1733
- Goldie et al., 1982Goldie, J.H., Coldman, A.J., and Gudauskas, G.A. Rationale for the use of altering non-cross-resistant chemotherapy. Cancer Treat. Rep. 1982; 66: 439–449
- Gottesman et al., 2002Gottesman, M.M., Fojo, T., and Bates, S.E. Multidrug resistance in cancer: role of ATP-dependent transporters. Nat. Rev. Cancer. 2002; 2: 48–58
- Haeno et al., 2012Haeno, H., Gonen, M., Davis, M.B., Herman, J.M., Iacobuzio-Donahue, C.A., and Michor, F. Computational modeling of pancreatic cancer reveals kinetics of metastasis suggesting optimum treatment strategies. Cell. 2012; 148: 362–375
- Hickey et al., 2013Hickey, B.E., Francis, D.P., and Lehman, M. Sequencing of chemotherapy and radiotherapy for early breast cancer. Cochrane Database Syst. Rev. 2013; 4: CD005212
- Holohan et al., 2013Holohan, C., Van Schaeybroeck, S., Longley, D.B., and Johnston, P.G. Cancer drug resistance: an evolving paradigm. Nat. Rev. Cancer. 2013; 13: 714–726
- Horiot et al., 1988Horiot, J.C., van den Bogaert, W., Ang, K.K., Van der Schueren, E., Bartelink, H., Gonzalez, D., de Pauw, M., and van Glabbeke, M. European Organization for Research on Treatment of Cancer trials using radiotherapy with multiple fractions per day. A 1978-1987 survey. Front. Radiat. Ther. Oncol. 1988; 22: 149–161
- Hryniuk, 2001Hryniuk, W. Dosage parameters in chemotherapy of breast cancer. Breast Dis. 2001; 14: 21–30
- Katouli and Komarova, 2011Katouli, A.A. and Komarova, N.L. The worst drug rule revisited: mathematical modeling of cyclic cancer treatments. Bull. Math. Biol. 2011; 73: 549–584
- Kimmel and Swierniak, 2006Kimmel, M. and Swierniak, A. Control theory approach to cancer chemotherapy: Benefiting from phase dependence and overcoming drug resistance. in: A. Friedman (Ed.) Tutorials in Mathematical Biosciences III. Springer, ; 2006: 185–221
- Lake and Hudis, 2004Lake, D.E. and Hudis, C.A. High-dose chemotherapy in breast cancer. Drugs. 2004; 64: 1851–1860
- Landau et al., 2013Landau, D.A., Carter, S.L., Stojanov, P., McKenna, A., Stevenson, K., Lawrence, M.S., Sougnez, C., Stewart, C., Sivachenko, A., Wang, L. et al. Evolution and impact of subclonal mutations in chronic lymphocytic leukemia. Cell. 2013; 152: 714–726
- Leder et al., 2014Leder, K., Pitter, K., Laplant, Q., Hambardzumyan, D., Ross, B.D., Chan, T.A., Holland, E.C., and Michor, F. Mathematical modeling of PDGF-driven glioblastoma reveals optimized radiation dosing schedules. Cell. 2014; 156: 603–616
- Ledzewicz and Schattler, 2009Ledzewicz, U. and Schattler, H. On the optimality of singular controls for a class of mathematical models for tumor anti-angiogenesis. Discrete Continuous Dyn. Syst. Ser. B. 2009; 11: 691–715
- Martin and Teo, 1993Martin, R.B. and Teo, K.L. Optimal Control of Drug Administration in Cancer Chemotherapy. World Scientific Pub Co Inc, ; 1993
- Martin et al., 1992Martin, R.B., Fisher, M.E., Minchin, R.F., and Teo, K.L. Optimal control of tumor size used to maximize survival time when cells are resistant to chemotherapy. Math. Biosci. 1992; 110: 201–219
- Murray and Coldman, 2003Murray, J.M. and Coldman, A.J. The effect of heterogeneity on optimal regimens in cancer chemotherapy. Math. Biosci. 2003; 185: 73–87
- Norton and Simon, 1977Norton, L. and Simon, R. Tumor size, sensitivity to therapy, and design of treatment schedules. Cancer Treat. Rep. 1977; 61: 1307–1317
- Pao et al., 2005Pao, W., Miller, V.A., Politi, K.A., Riely, G.J., Somwar, R., Zakowski, M.F., Kris, M.G., and Varmus, H. Acquired resistance of lung adenocarcinomas to gefitinib or erlotinib is associated with a second mutation in the EGFR kinase domain. PLoS Med. 2005; 2: e73
- Paridaens et al., 2003Paridaens, R., Van Aelst, F., Georgoulias, V., Samonnig, H., Cocquyt, V., Zielinski, C., Hausmaninger, H., Willemse, P., Boudraa, Y., Wildiers, J. et al. A randomized phase II study of alternating and sequential regimens of docetaxel and doxorubicin as first-line chemotherapy for metastatic breast cancer. Ann. Oncol. 2003; 14: 433–440
- Recht et al., 1996Recht, A., Come, S.E., Henderson, I.C., Gelman, R.S., Silver, B., Hayes, D.F., Shulman, L.N., and Harris, J.R. The sequencing of chemotherapy and radiation therapy after conservative surgery for early-stage breast cancer. N. Engl. J. Med. 1996; 334: 1356–1361
- Sawyers, 2004Sawyers, C. Targeted cancer therapy. Nature. 2004; 432: 294–297
- Sharma et al., 2011Sharma, P., Wagner, K., Wolchok, J.D., and Allison, J.P. Novel cancer immunotherapy agents with survival benefit: recent successes and next steps. Nat. Rev. Cancer. 2011; 11: 805–812
- Shrager and Tenenbaum, 2014Shrager, J. and Tenenbaum, J.M. Rapid learning for precision oncology. Nat. Rev. Clin. Oncol. 2014; 11: 109–118
- Stiehl et al., 2015Stiehl, T., Baran, N., Ho, A.D., and Marciniak-Czochra, A. Cell division patterns in acute myeloid leukemia stem-like cells determine clinical course: a model to predict patient survival. Cancer Res. 2015; 75: 940–949
- Van Loo and Voet, 2014Van Loo, P. and Voet, T. Single cell analysis of cancer genomes. Curr. Opin. Genet. Dev. 2014; 24: 82–91
- Zhao et al., 2014Zhao, B., Hemann, M.T., and Lauffenburger, D.A. Intratumor heterogeneity alters most effective drugs in designed combinations. Proc. Natl. Acad. Sci. USA. 2014; 111: 10773–10778
http://blog.sciencenet.cn/blog-349513-938321.html 此文来自科学网杨波博客,转载请注明出处。