《明捷数学随谈:挑战极限的人(2)拓扑学的奇思妙想》
By 明捷
明捷是我的高中同学,跳级来到我们高中的尖子班,学霸。令人瞩目的是数学成绩格外突出,这一定有遗传的因素,明捷的父亲是大学数学教授,母亲是高中数学教师。在1980年的高考中,明捷的成绩名列前茅。他就读于中国科技大学,后来又在中美两国获得硕士和博士学位。目前他在最著名的汽车公司工作,业余时间,还会对数学念念不忘。在高中微信群里,他写了一些在数学领域挑战极限的人和事,十分有趣,大家建议他整理成文,发表出来,让更多的人看到。不负众望,一篇《明捷数学随谈:挑战极限的人》一文,应运而生了。他没有注册任何网站,我就受他之托,将此文分享给大家。下面就是全文之二:拓扑学的奇思妙想。
【五.欧拉和图论的产生】
18世纪早期,东欧位于现俄罗斯境内有一个叫做柯尼期堡的小城。城中有一条河流过,形成了一个小岛,有7座石桥将小岛及河的对岸相连。城中的居民闲暇时喜欢到小岛上散步。久而久之,有人想搞点事情,他们声称,是否能找到一条散步路线,可以经过这7座桥,而且每座桥只经过一次?越来越多的人开始尝试这个挑战,但都没有成功。

(七座桥和图论)
于是他们找到了时任俄罗斯皇家科学院院士的大数学家欧拉,请他帮忙找一个方法。欧拉告诉他们,这可以归结为一个数学问题,在这个问题中,桥的长度,位置以及城区的面积等等都不重要。他将每座桥用一条线来代替,而每块陆地则用一个点来代替,在这个抽象后的问题中,重要的是整个图形的连通性。欧拉对这个抽象的模型用了一些逻辑分析,然后告诉柯尼斯堡的居民说,你们想要的那个一次性走完7座桥的方法是不存在的。欧拉的这个方法,形成了一个新的数学分支:图论。

(欧拉)
【六.拓扑学的来历】
欧拉借柯尼斯堡七桥问题开创了图论。他这种在处理区域问题时忽略具体形状,尺寸,位置而突出联通性的思想在100多年后被人引伸,形成了现代数学的一个活跃的新分支:拓扑学。从拓扑学的角度看一个空间区域,传统几何学中的尺寸,距离,角度等概念都消失了。一个立方体面和一个球面,不论大小,都是拓扑等价的,但一个球面和一个轮胎面则不是等价的,因为轮胎孔改变了区域的流通性。拿一团面揉揉,做成一个馒头;或者把它扭一下,做成一个花卷;再或者把它先拉得细长,再扭一下,做成一根油条。在拓扑学家看来,这些没有差别。但如果把这团面做成面窝(武汉人都知道,面窝其实不是用面做的),在拓扑上就不同了,因为中间挖了一个孔,联通性变了。有人也许会说,这些数学家太喜欢搞事情了,本来几何学就已经够让人头痛了,现在又整出个拓扑学,有啥用呢?
拓扑学在刚开始时完全是出于数学家的兴趣,没有实际用途。但随着时间的推移,逐渐开始应用在科学,工程和医学上。科学家们尝试用拓扑图形来解释广义相对论所预测的宇宙空间。在工程结构分析行业中,有一种方法称为拓扑优化,被广泛地应用于各种工程结构的设计中。例如设计一种飞机的机翼,先简单地将它设计成实心的,把根据空气动力学方法计算出来的外力加在这个机翼上,得到内部应力的分布,然后挖去应力较小部位的材料,就形成了一个空心机翼,这样即保证了机翼的强度,又实现了结构轻量化。这项技术需要用到拓扑变换的概念。
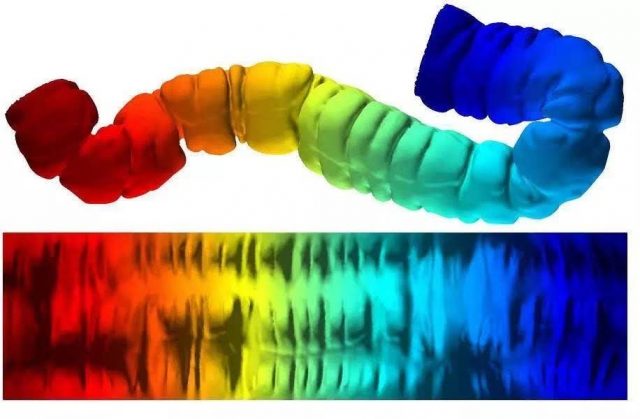
近年来在医学上出现了一种称为虚拟肠镜的技术,即通过扫描得到人体大肠的一组剖面图,然后用拓扑分析的方法寻找大肠内可能的肿瘤。数学家还试图将拓扑学应用在人体整形中。
【七.庞加莱猜想与佩雷尔曼】
150多年前诞生的法国数学家庞加莱被称为现代拓扑学之父,他也被一些人尊为近代最伟大的数学家。"最伟大"这个词常常会让人表示不服,但庞加莱至少是近代数学界东邪,西毒,南帝,北丐一类的人物。1900年,庞加莱提出,能否将曲面的拓扑等价性推广到更高维空间中。例如,我们现在知道一只兔子的体表面和球面是拓扑等价的,那么在高一维的空间中,这种等价性是否也成立呢?这个想法让问题变得相当抽象。兔子的外表面和球面是我们肉眼能看见的,但高维空间中曲面是什么样的,谁能想象呢?

(庞加莱)
中央电视台曾邀请数学大师丘成桐教授做了一个一小时左右的节目,节目中丘教授展示了一张由计算机模拟得到的高维曲面,神秘而美幻。当时有观众考了丘教授一个智力题,用到加减乘除运算,丘教授没有答上来,他打趣地说,数学家的算术都不好。总之,庞加莱提出的这个命题相当抽象,被公认为20世纪7大数学难题之一。

(丘成桐)
庞加莱的猜想提出后,接下来30多年里在数学界并没有引起什么动静,也许那时学科的发展还没有达到解决这个问题的门槛。庞加莱在1912年58岁时就去世了,他大概想像不到100年后,他的这个猜想在数学界激起的一系列波澜。
庞加莱猜想提出约半世纪后,陆续有人声称给出了证明,但接着就被推翻。直到上世纪末,坚硬的冻土开始有些松动。2000年,美国格雷数学研究所将庞加莱猜想列为千禧年难题,悬赏一百万美元寻求最终的证明。一石激起千层浪,世界各地的数学家们由此预感到了契机,纷纷出山,意欲逐鹿中原。一时间江湖上风声鹤唳,剑拔弩张。终于在两三年后,一代大侠横空出世,俄罗斯人佩雷尔曼率先在互联网上宣布,证明了庞加莱猜想。他没有按常规将论文投到正规的学术期刊由专家审稿,而是直接在一个网站上登了出来。

(佩雷尔曼)
说起这个佩雷尔曼,原非等闲之辈。他于1966年出生于前苏联一个犹太人家庭,父亲是工程师,母亲是数学老师。1982年,16岁的佩雷尔曼参加国际奥数大赛,得了满分,为前苏联赢得一枚金牌。高中毕业后他获免试进入圣彼得堡大学,在数学专业一直读到博士毕业,然后进了当地的一个数学研究所工作。1991年,前苏联解体,佩雷尔曼的父亲决定移民以色列,但他母亲坚决不肯移民。于是他父亲带着他妹妹去了以色列,他和母亲留在圣彼得堡。上世纪九十年代,佩雷尔曼有几年时间游学美国,其间曾轻而易举地解决了一个公开的数学难题。美国几所顶尖名校表示愿意聘他为助理教授,但他嫌职位太低,不予接受。在一次聚会上,他和一名叫汉密尔顿的年青数学家交谈,对方告诉他自己正在研究庞加莱猜想,这激发了他的兴趣,他决定返回圣彼得堡,开始对庞加莱猜想的研究。
以后10多年发生的事情表明,佩雷尔曼是一个视名利如粪土的人。他决定解决庞加莱猜想,完全出于专业上的兴趣,和获大奖及高额赏金无关。在那次聚会上和汉密尔顿的偶然交谈,使他在无意中卷入了世纪之交的那场群雄争霸的场面。在潜心研究庞加莱猜想几年后,到了2002年,佩雷尔曼确认自己大功告成。他匿名在互联网上宣布:庞加莱猜想已被证明!同时将无署名的论文发布在公开网战上。开始人们以为这是个恶作剧,但仔细读了他的论文后,发现此人功夫深不可测。有人猜到这可能是佩雷尔曼干的。一时间各大学术网站沸腾了,有人为这个消息感到欢欣鼓舞,也有人顿首捶胸,不甘心自己多年的心血付之泡影,竟被一个无名人士抢了先。于是佩雷尔曼的论文受到一些人的怀疑和挑战。在让子弹飞了一会儿后,佩雷尔曼现身,承认是他搞的事情。但他不回覆任何质疑和挑战,认定自己给出的是最终的证明。
在对佩雷尔曼的论文进行了历经四年的严格评审后,国际数学届正式于2006年认定这是对庞加莱猜想的最终证明。同年,国际数学联盟决定授予佩雷尔曼以费尔兹奖。费尔兹奖每四年评选一次,人们常将它比作数学界的诺贝尔奖。顺便说一句,丘成桐教授是第一位获费尔兹奖的华人。另一位华人得奖者是生长于澳洲的天才数学家陶哲轩,他现为加州大学洛杉矶分校的教授。
令人相当不解的是,当佩雷尔曼得知国际数学联盟要授予他费尔兹奖时,他明确表示不会接受。这时他已经离开了原来的工作单位,成为无业人员,和老母亲住在一起,相依为命。至于他为什么离开了原来的研究所,众说纷纭。有人说他因为专注于庞加莱猜想的研究,好几年都没有发表一篇论文,通不过单位的年终考核,受到同事的排挤而离开。还有人说他证明了庞加莱猜想后,单位领导说可以为他申报俄罗斯科学院院士,他不以为然,得罪了领导,就辞职不干了。失业后,他的生活很贫困,据邻居说,他家里只有几件简陋的傢俱,穿的毛衣上也是破洞。国际数学联盟派专人到他家里,试图说服他同意接受该奖项,被他当面拒绝了。尽管如此,费尔兹奖的授奖仪式仍在当年西班牙主办的国际数学家大会上如期举行,西班牙国王受邀成为颁奖嘉宾。颁奖当天,人们期待佩雷尔曼会突然现身,然而没有。当大会主席宣布将费尔兹奖授予佩雷尔曼时,会堂里仍然响起了热烈的掌声。
事后有人说,佩雷尔曼不去西班牙领奖,是因为没有路费。但这显然说不通,若他真想去,区区几百美元路费,找国际数学联盟要点资助不就行了。接下来发生的事更让人瞠目结舌。2010年,格雷数学研究所决定覆行承诺,将100万美元的千禧年大奖授于佩雷尔曼,再次被他拒绝了,理由是汉密尔顿应该和他共享这项奖,否则不公平。至此,佩雷尔曼完全从公众的视线中消失了。后来纽约时报发了一篇报道,讲述他的故事,说他放弃了百万美元大奖,而宁愿在俄罗斯的森林里采蘑菇。