金碧辉煌的圣殿(4. Never say never)The Magnificent Temple (4.)
在欧氏几何这两千多年的发展史上,共圆(cocircular)问题一直是一个十分有趣的话题,这方面的大量的定理和命题被发现,极大地丰富了人们对图形的认知。稍有几何知识的人都知道,三点如果不在一条直线上,则总是共圆的。四点若要共圆则需要一些条件,比如四点构成的四边形的对角的角度之和为180度,这是四点共圆的充分必要条件。
In the more than two thousand years of the development of Euclidean geometry, the problem of cocircularity has always been an intriguing topic. Numerous theorems and propositions in this area have been discovered, significantly enriching people's understanding of geometric shapes. Anyone with a basic knowledge of geometry knows that if three points are not on the same line, they are always cocircular. For four points to be cocircular, certain conditions are required, such as the sum of the angles formed by the diagonals of the quadrilateral being 180 degrees, which is a sufficient and necessary condition for four points to be cocircular.
若是更多的点共圆,有时情况就比较“邪乎”了。例如非常有趣且著名的“九点圆定理”(nine-point circle theorem)是法国数学家Olry Terquem 在几代人结果的基础上,于200年前最终揭示的。九点圆定理的表述也非常简洁:“任意三角形三高线的垂足、各边中点、各顶点与垂心连线的中点,这九个点共圆。”(The midpoint of each side of the triangle, the foot of each altitude and the midpoint of the line segment from each vertex to the orthocenter all lie on the same circle. )
When it comes to more points being cocircular, things can get a bit "weird." For instance, the fascinating and famous "Nine-Point Circle Theorem" was revealed by the French mathematician Olry Terquem about 200 years ago, building on the results of several generations. The theorem is succinctly stated as follows: "The midpoint of each side of the triangle, the foot of each altitude, and the midpoint of the line segment from each vertex to the orthocenter all lie on the same circle."
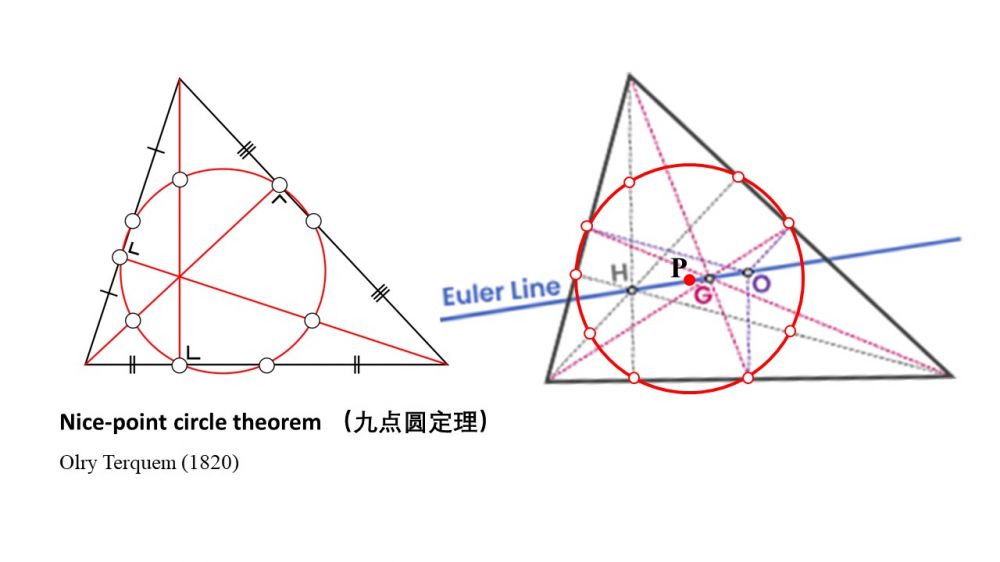
很神奇是不是?其实远远不止于此。比如,这个“九点圆”的半径是同一个三角形外接圆半径的一半;这个圆分别与同一个三角形的三个旁切圆外切。而且,这个圆的圆心一定在欧拉线上。上一篇我们提到了欧拉线。现在有人误以为欧拉也发现了九点圆。其实不是的,他生前没有看出来。
Isn't it amazing? In fact, it goes far beyond this. For instance, the radius of this "Nine-Point Circle" is half the radius of the circumcircle of the triangle. This circle is also tangent to the three excircles of the same triangle. Moreover, the center of this circle must lie on the Euler line, which was mentioned in the last article of this series. Contrary to popular belief, Euler did not discover the Nine-Point Circle during his lifetime.
对中国的几何爱好者来说,名气最大的不是上面那个九点圆,而是1838年由法国数学家Auguste Miquel 发现并证明的的“五点共圆定理”(Miquel's Pentagram Theorem )。结合下图,这个定理的表述也非常简明:任意一个五角星形(不要求正五角星),分别对其五个三角形做外接圆,则外侧的五个交点共圆。(There are five triangles externally to the pentagon. Construct the five circumcircles. Each pair of adjacent circles intersect at a vertex of the pentagon and a second point. The five second points are concyclic.)
For geometry enthusiasts in China, the most famous theorem is not the Nine-Point Circle mentioned above, but the "Five-Point Cocircularity Theorem" discovered and proven by the French mathematician Auguste Miquel in 1838. With reference to the diagram below, the theorem is succinctly stated: "For any pentagram (not necessarily regular), construct the circumcircles for each of its five triangles; then, the outer five intersection points are cocircular."
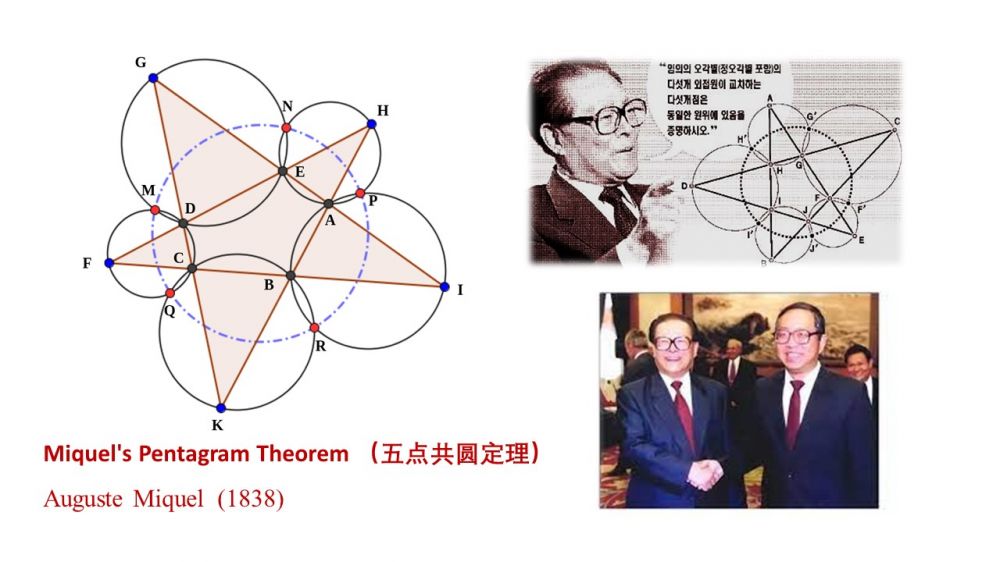
这个定理之所以今年在中国大陆有名,是因为一年前去世的前国家主席江泽民。他是工科出身,也是一位数学爱好者。据他说,求证“五点共圆定理”是他当年考大学的一道题。(水平了得!)于是他多次拿出来考人。他接见中国IMO队时提到这道题,还打电话到中科院院士张景中家里讨论这道题,弄得老张一脑门子汗。最有名的一次是2000年12月20日,江主席在澳门出席澳门特别行政区成立一周年庆祝活动,并参观濠江中学。他即兴给同学们出了这道题,并亲自到黑板上画图。濠江中学师生很少做这么难的题,圣诞都没过踏实,全校攻关,终于在12月28号得证,算过了一个踏实的新年。其实早在5年前,哈佛大学数学系教授、菲尔兹奖获得者丘成桐访问中国时,江主席就从兜里面摸出这道题让他证明。老邱一看就晕菜了,心想您这是让将军挖战壕啊。他回到宾馆闭门苦思,终于能在第二天离京前能够给中办一条信息:请转告江主席,他出的题我证出来了,Oh yeah!!!
This theorem gained prominence in mainland China this year because of the passing of former Chinese President Jiang Zemin. With a background in engineering, he was also a mathematics enthusiast. According to him, proving the "Five-Point Cocircularity Theorem" was a question in his university entrance exam (such a high level!). He frequently presented this problem to others. He mentioned this problem when he met Chinese IMO team, and he even discussed it with academician Zhang Jingzhong of the Chinese Academy of Sciences, causing some stress for Zhang. One notable instance occurred on December 20, 2000, when President Jiang, during his visit to Macau for the celebration of its first anniversary as a Special Administrative Region, spontaneously posed this problem to students at Ho Fai High School, and personally drew the diagram on the blackboard. The students at the High School were not accustomed to tackling such challenging problems, and their Christmas was far from peaceful as the entire school collaborated to solve it. Eventually, on December 28, they succeeded, marking a satisfying end to the year. In fact, five years earlier, when Harvard University mathematics professor and Fields Medalist Shing-Tung Yau visited China, President Jiang pulled out this problem from his pocket and asked Yau to prove it. Yau, feeling a bit overwhelmed, returned to his hotel room and, after intense contemplation, was able to send a message to the Central Office the next day: Please convey to President Jiang that I have proven the problem he posed. Oh yeah!!!
这些事情,有时都造成了国际影响了。比如濠江中学出题这事儿,韩国媒体就报道了:您瞧人家中国主席多睿智、多有学问。再看看俺们青瓦台的那几块料,除了玩政治还会啥?…… 去年江主席去世的时候,很多人,包括我本都反省,当年我们笑话他爱卖弄,抨击他独裁,有点不公平啊。他肚子里有货,有资格卖弄嘛。而他当政那时候毕竟给我们一点抨击、说怪话空间啊…… 不怕不识货,就怕货比货!
These occurrences sometimes create international impact. For instance, when the problem from Ho Fai High School was publicized, Korean media reported: Look at how wise and knowledgeable the President of China is compared to our Blue House, those in it know how to play politics. Last year, when President Jiang passed away, many people, including myself, reflected on the fact that we had mocked him for showing off and criticized him for being authoritarian. It seems a bit unfair now. He had substance, and he had the qualifications to show off. During his presidency, he at least gave us some room for criticism and bizarre remarks… It's not about not recognizing quality; it's about comparing quality!
扯远了。我们回来聊几何。我们前两次说的Morley’s trisector theorem 和 John’s theorem 分别是在19和20世纪才被发现的。虽然欧氏几何就像一座特殊的金矿,总能有耀眼的金块被发现,但到了21世纪,在欧氏几何被人类学习、研究了2400年后,人们还能发现简单的几何规律吗?
You bet it!
Let's get back to geometry. The two theorems we discussed in my earlier articles, Morley's Trisector Theorem and John's Theorem, were discovered in the 19th and 20th centuries, respectively. Although Euclidean geometry is like a special gold mine where dazzling nuggets are always discovered. As we entered the 21st century, after 2400 years of humans studying and researching Euclidean geometry, can we still find simple geometric laws?
You bet it!
时间到了2000年。在荷兰的南部海滨有个叫Zeeland的小地方,一位年轻的高中数学老师叫Floor van Lamoen。本来中学老师照本宣科就行了,但这位van Lamoen先生是个数学迷,爱琢磨事儿,他时常在欧氏几何和初等数论方面有些小进展、小发表(不是大数学家那种)。我们都知道任何三角形顶角与对边的中点连成中线,三条中线交于重心G,把三角形分成面积相等的6块。他对6个小三角形分别做外接圆,惊奇地发现6个圆的圆心似乎是共圆的。他将三角形的形状作了多种变换,从图形上看,这个规律几乎肯定是存在的。
Fast forward to the year 2000. In the southern coastal region of the Netherlands, there is a small place called Zeeland, where a young high school math teacher named Floor van Lamoen resides. Usually, high school teachers follow the curriculum, but Mr. van Lamoen is a math enthusiast who likes to ponder. He often makes small advances and publications in Euclidean geometry and elementary number theory (not at the level of renowned mathematicians). We all know that connecting the vertex of any triangle with the midpoint of the opposite side forms a median. The three medians intersect at the centroid G, dividing the triangle into six regions of equal area. He constructed circumcircles for the six small triangles and was amazed to find that the centers of the six circles seemed to be cocircular. He experimented with various transformations of the triangle's shape, and from a graphical perspective, this pattern almost certainly existed.
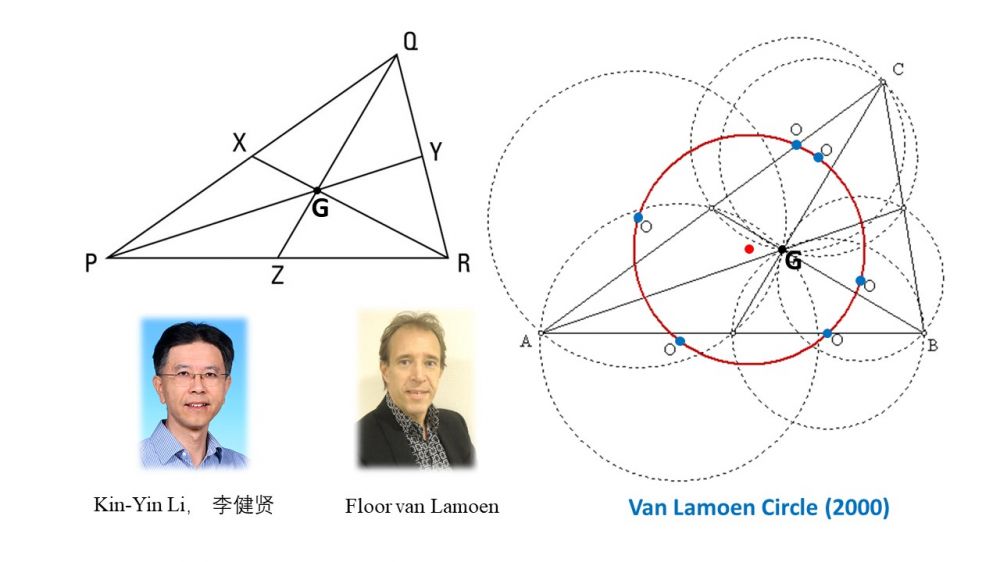
然而在试图证明时,van Lamoen却被卡住了,努力好几个月居然未能攻克。这个六点共圆问题的确是不太好证的。相比较而言,前面那个“九点圆定理”倒是比较好证。
However, when attempting to prove it, Mr. van Lamoen got stuck and, despite months of effort, couldn't overcome the challenge. The problem of six points being cocircular was indeed not easy to prove. Comparatively, the earlier "Nine-Point Circle Theorem" was easier.
于是van Lamoen考虑再三,决定把它作为一个open problem征答。他将问题登在了American Mathematical Monthly 2000年11月号的Problems栏目中。在阅读这个问题的人中间,有一个人叫 Kin-Yin Li,中文名叫李健贤。他当时是香港科技大学的年轻数学教授,几年前刚刚从加州伯克利拿了数学博士学位,回港加盟香港科技大学数学系。这位李博士是个解难题的人。而且 此前几年,IMO有一年在香港举行。借着这个东风,包括李健贤在内的一些促进香港竞赛数学的人士创办了一个竞赛数学的News Letter,叫Mathematical Excalibur。当时李健贤是它的编辑和重要撰稿人,后来他成了香港竞赛数学的教父级人物。
So, after serious consideration, van Lamoen decided to pose it as an open problem. He published the problem in the "Problems" section of the November 2000 issue of the American Mathematical Monthly. Among those reading the problem was a person named Kin-Yin Li, also as 李健贤in Chinese. At the time, he was a young mathematics professor at the Hong Kong University of Science and Technology, having recently earned a Ph.D. in mathematics from the University of California, Berkeley. Dr. Li is someone skilled at solving problems. Moreover, in the previous years, an International Mathematical Olympiad (IMO) had been held in Hong Kong. Taking advantage of this, Dr. Li and other enthusiasts promoting mathematical competitions in Hong Kong established a newsletter called "Mathematical Excalibur." At that time, Dr. Li served as its editor and a significant contributor. Later, he became a key figure in the world of mathematical competitions in Hong Kong.
李健贤马上就看到了van Lamoen的问题。这个问题难不住他,他很快得到证明。的确,证明不是很简单,他用了几乎一页纸的篇幅。他的证明登在了2001年春天的一期Mathematical Excalibur上,正式成为了定理。现在这个圆依然叫“Van Lamoen Circle”,李博士并没有表面上的名分,他也不需要。有趣的是(见下图),他在解这道题之前,先提到了江泽民主席在澳门濠江中学出的那道题。该题与van Lamoen问题的提出时间相近,李博士也注意到了,于是先评论一下。
Dr. Li immediately noticed van Lamoen's problem. It didn't stump him, and he quickly provided a proof. Indeed, the proof was not very straightforward, taking up almost a full page. His proof was published in the spring issue of Mathematical Excalibur in 2001, officially becoming a theorem. The circle associated with this discovery is still called the "Van Lamoen Circle," and Dr. Li did not seek surface recognition for it, nor did he need to. Interestingly (as seen in the image below), before tackling this problem, Dr. Li mentioned the problem posed by President Jiang Zemin at in Macau. The timing of this problem's proposal was close to that of van Lamoen's, and Dr. Li took note of it, providing some comments beforehand.

那么,今后人们还会继续有这样的发现吗?应该说,欧氏几何发展到今天,新发现的机会越来越小了,但可能性依然是存在的。也许将来某一天,一名爱好者或者业余数学家,在不经意之间,能再次揭示出某一条简明而优美的欧氏几何规律……
Never say never.
So, will people continue to make such discoveries in the future? It must be said that as Euclidean geometry has been studied and researched by humans for 2400 years, the chances of new discoveries are diminishing. However, the possibility still exists. Perhaps one day, an enthusiast or amateur mathematician will, inadvertently, reveal another concise and elegant Euclidean geometric law...
Never say never.
[Edited from ChatGPT translation]