别人推荐的书,我就去图书馆借来看。
书名:The Curious Incident of the Dog in the Night-time
作者: Mark Haddon
前一阵子大家都为自闭担心,我也不例外,因为豆豆虽然不符合大部分的症状,但是他的确有语言发育迟缓,喜欢排直线这些问题。我想多了解自闭症,所以就找这本书来看一看。
这本书其实写得挺好看,因为是侦探小说,作者是带着读者一步一步把谜团解开的。故事是由一只被杀的狗引起的。叙述者是一个十五岁的自闭少年。
书的扉页这样介绍:
Christopher John Francis Boone知道世界上所有国家的名字和其首府,他还可以数到7,057的质数。
他喜欢狗可是无法了解人的情绪。他不能接受别人触摸他的身体。虽然Christopher 有个非凡而逻辑性强的脑子,他患有自闭症。 etc...
Christopher 不喜欢和别人作正常交流,别人问他话,他可以答出来,如果你和他聊天 (chit-chat)他就无法奉陪了。时间表和日常规律对他非常重要。他每天的作息安排是要精准到以分钟计算的。他只吃某种食物,因为有些食物的颜色让他和一些他有痛苦记忆的事件联系起来。
他的记忆力非常好,他记得从记事以来所有的人、事、地点和时间。但是这也是个缺点:他不会像常人那样自动过滤我们认为不重要的人和物。
他不喜欢看人的脸,因为人的表情千变万化,他不能及时吸收处理并理解这些表情要表达的信息。(这就是为什么自闭儿不喜欢眼神接触。) Christopher 喜欢熟悉的环境,因为他喜欢知道所有的东西的位置,了解周围的环境,让他感觉安全。到了一个新环境,他有太多的东西要吸收,太多的东西要记忆,这让他感到非常痛苦。他对付这个痛苦的方式是按住自己的双耳,倒在地上大声呻吟。这样做,可以帮助他屏蔽外界的干扰,减轻痛苦。
Christopher 痛恨/惧怕身体接触,他和父母也不拥抱,他的父母对他表达爱的方式是把一只手像一把扇子那样摊开,然后他也摊开手掌,接触指尖。
书里说了一个Christopher 最喜欢的梦,让我看了有触目惊心的感觉。Christopher 的梦是这样的:有一天,世界上大部分的人因为染了一种病毒,都快死光了。最后只剩下那些和他一样不喜欢看别人脸,也不了解这些图画的意思的人。



然后他就可以随心所欲的到别人家里和店里拿东西吃,拿衣服穿和玩电玩。
这本书其实写得很不错,由Christopher 的侦探"事业"的推进,揭发了一个重大的秘密,让他了解了他父母的婚姻和他妈妈的死亡真像。书里对Christopher 的心理有细致的描写,让我们可以走进一个自闭儿的内心,了解他们的想法。Christopher 可能属于 highly functional 了,懂行的人说一说吧。
作者年轻的时候长期和自闭儿待在一起(书上说是 As a young man, Haddon worked with autistic individuals),所以对自闭儿的观察细致,有深刻的了解。作者是英国人,所以很多英国的习惯用语,像 bloody something something,我因为看惯了美国人写的书,所以察觉了这些差异。
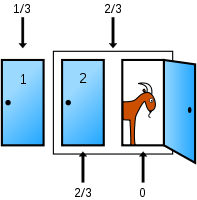
书中还有不少关于逻辑和数学的题目探讨。我在这里列一个我认为挺有意思的经典题目,叫"The Monty Hall Problem"
From Wikipedia:
The Monty Hall problem is a probability puzzle loosely based on the American television game show Let's Make a Deal. The name comes from the show's host, Monty Hall. The problem is also called the Monty Hall paradox, as it is a veridical paradox in that the solution is counterintuitive.
A well-known statement of the problem was published in Parade magazine:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice? (Whitaker 1990)
Because there is no way for the player to know which of the two unopened doors is the winning door, most people assume that each door has an equal probability and conclude that switching does not matter. In fact, in the usual interpretation of the problem the player should switch—doing so doubles the probability of winning the car, from 1/3 to 2/3.
When the problem and the solution appeared in Parade, approximately 10,000 readers, including nearly 1,000 with Ph.D.s, wrote to the magazine claiming the published solution was wrong. Some of the controversy was because the Parade version of the problem is technically ambiguous since it leaves certain aspects of the host's behavior unstated, for example whether the host must open a door and must make the offer to switch. Variants of the problem involving these and other assumptions have been published in the mathematical literature.
The standard Monty Hall problem is mathematically equivalent to the earlier Three Prisoners problem and both are related to the much older Bertrand's box paradox.
These and other problems involving unequal distributions of probability
are notoriously difficult for people to solve correctly, and have led
to numerous psychological studies. Even when given a completely
unambiguous statement of the Monty Hall problem, explanations,
simulations, and formal mathematical proofs, many people still meet the
correct answer with disbelief.
Problem
Steve Selvin wrote a letter to the American Statistician in 1975 describing a problem loosely based on the game show Let's Make a Deal (Selvin 1975a). In a subsequent letter he dubbed it the "Monty Hall problem" (Selvin 1975b). The problem is mathematically equivalent (Morgan et al., 1991) to the Three Prisoners Problem described in Martin Gardner's Mathematical Games column in Scientific American in 1959 (Gardner 1959a).
Selvin's Monty Hall problem was restated in its well-known form in a letter to Marilyn vos Savant's Ask Marilyn column in Parade:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice? (Whitaker 1990)
There are certain ambiguities in this formulation of the problem: it is unclear whether or not the host would always open another door, always offer a choice to switch, or even whether he would ever open the door revealing the car (Mueser and Granberg 1999). The standard analysis of the problem assumes that the host is indeed constrained always to open a door revealing a goat, always to make the offer to switch, and to open one of the remaining two doors randomly if the player initially picked the car (Barbeau 2000:87). Hence a more exact statement of the problem is as follows:
Suppose you're on a game show and you're given the choice of three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed randomly behind the doors before the show. The rules of the game show are as follows: After you have chosen a door, the door remains closed for the time being. The game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two remaining doors, and the door he opens must have a goat behind it. If both remaining doors have goats behind them, he chooses one randomly. After Monty Hall opens a door with a goat, he will ask you to decide whether you want to stay with your first choice or to switch to the last remaining door. Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?" Is it to your advantage to change your choice? (Krauss and Wang 2003:10)
Note that the player may initially choose any of the three doors (not just Door 1), that the host opens a different door revealing a goat (not necessarily Door 3), and that he gives the player a second choice between the two remaining unopened doors.
Discussion
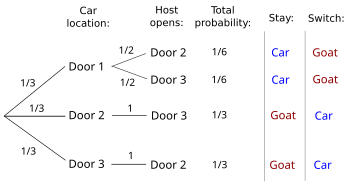
The overall probability of winning by switching is determined by the location of the car. Assuming the problem statement above and that the player initially picks Door 1:
- The player originally picked the door hiding the car. The game host must open one of the two remaining doors randomly.
- The car is behind Door 2 and the host must open Door 3.
- The car is behind Door 3 and the host must open Door 2.
Players who choose to switch win if the car is behind either of the
two unchosen doors rather than the one that was originally picked. In
two cases with 1/3 probability switching wins, so the overall
probability of winning by switching is 2/3 as shown in the diagram
below. In other words, there is a 2/3 chance of being wrong initially, and thus a 2/3 chance of being right when changing to the other door.
The reasoning above applies to all players at the start of the game
without regard to which door the host opens, specifically before the
host opens a particular door and gives the player the option to switch
doors (Morgan et al. 1991).
This means if a large number of players randomly choose whether to stay
or switch, then approximately 1/3 of those choosing to stay with the
initial selection and 2/3 of those choosing to switch would win the
car. This result has been verified experimentally using computer and
other simulation techniques (see Simulation below).
A subtly different question is which strategy is best for an individual player after being shown a particular open door. Answering this question requires determining the conditional probability of winning by switching, given which door the host opens. This probability may differ from the overall probability of winning depending on the exact formulation of the problem (see Sources of confusion, below).
Referring to the figure above or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138) and considering only the cases where the host opens Door 2, switching loses in a 1/6 case where the player initially picked the car and otherwise wins in a 1/3 case. Similarly if the host opens Door 3 switching wins twice as often as staying, so the conditional probability of winning by switching given either door the host opens is 2/3 — the same as the overall probability. A formal proof of this fact using Bayes' theorem is presented below (see Bayesian analysis).
Summary and Solution
There are three doors. Two doors have a goat behind them and one door has a car behind.
(Remember goat is bad and car is good)
1) Choose one door
2) Game host opens one door containing a goat
3) Do you change door?
For example:
| Door 1 | Door 2 | Door 3 |
|---|---|---|
| Goat | Goat | Car |
Now you have two opions: switch or not switch
Not switch
| pick | show | outcome |
|---|---|---|
| 1 | 2 | lose |
| 2 | 1 | lose |
| 3 | 2 or 1 | win |
If you do not switch the probability of winning is 1/3
Switch
| pick | show | outcome |
|---|---|---|
| 1 | 2 | win |
| 2 | 1 | win |
| 3 | 2 or 1 | lose |
If you switch the probability of winning is 2/3
You should therefore choose to switch doors
Sources of confusion
When first presented with the Monty Hall problem an overwhelming majority of people assume that each door has an equal probability and conclude that switching does not matter (Mueser and Granberg, 1999). Out of 228 subjects in one study, only 13% chose to switch (Granberg and Brown, 1995:713). In her book The Power of Logical Thinking, vos Savant (1996:15) quotes cognitive psychologist Massimo Piattelli-Palmarini as saying "... no other statistical puzzle comes so close to fooling all the people all the time" and "[realize] that even Nobel physicists systematically give the wrong answer, and that they insist on it, and they are ready to berate in print those who propose the right answer."
Most statements of the problem, notably the one in Parade Magazine, do not match the rules of the actual game show (Krauss and Wang, 2003:9), and do not fully specify the host's behavior or that the car's location is randomly selected (Granberg and Brown, 1995:712). Krauss and Wang (2003:10) conjecture that people make the standard assumptions even if they are not explicitly stated. Although these issues are mathematically significant, even when controlling for these factors nearly all people still think each of the two unopened doors has an equal probability and conclude switching does not matter (Mueser and Granberg, 1999). This "equal probability" assumption is a deeply rooted intuition (Falk 1992:202). People strongly tend to think probability is evenly distributed across as many unknowns as are present, whether it is or not (Fox and Levav, 2004:637).
A competing deeply rooted intuition at work in the Monty Hall problem is the belief that exposing information that is already known does not affect probabilities (Falk 1992:207). This intuition is the basis of solutions to the problem that assert the host's action of opening a door does not change the player's initial 1/3 chance of selecting the car. For the fully explicit problem this intuition leads to the correct numerical answer, 2/3 chance of winning the car by switching, but leads to the same solution for other variants where this answer is not correct (Falk 1992:207).
Another source of confusion is that the usual wording of the problem statement asks about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open if the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991).
Aids to understanding
Why the probability is not 1/2
The most commonly voiced objection to the solution is that the past can be ignored when assessing the probability—that it is irrelevant which doors the player initially picks and the host opens. However, in the problem as originally presented, the player's initial choice does influence the host's available choices subsequently.
This difference can be demonstrated by contrasting the original problem with a variation that appeared in vos Savant's column in November 2006. In this version, Monty Hall forgets which door hides the car. He opens one of the doors at random and is relieved when a goat is revealed. Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006).
In this version of the puzzle, the player has an equal chance of winning whether switching or not. Assuming the player picks Door 1 there are six possible outcomes that can occur, each with probability 1/6:
| Player picks Door 1 | ||||||
|---|---|---|---|---|---|---|
| Car behind Door 1 | Car behind Door 2 | Car behind Door 3 | ||||
| Host opens: | Door 2 | Door 3 | Door 2 | Door 3 | Door 2 | Door 3 |
| Host reveals: | Goat | Goat | Car | Goat | Goat | Car |
| Switching: | loses | loses | ? | wins | wins | ? |
In two cases above, the host reveals the car. What might happen in these cases is unknown—perhaps the contestant immediately wins or immediately loses. However, in the problem as stated, the host has revealed a goat, so only four of the six cases remain possible, and they are equally likely. In two of these four cases, switching results in a win, and in the other two, switching results in a goat. Staying with the original pick gives the same odds: a loss in two cases and a win in two others.
The player's probability of winning by switching increases to 2/3 in the original problem because in the two cases above where the host would reveal the car, he is forced to reveal the remaining goat instead. In the table below, these two cases are highlighted:
| Player picks Door 1 | ||||||
|---|---|---|---|---|---|---|
| Car behind Door 1 | Car behind Door 2 | Car behind Door 3 | ||||
| Host opens: | Door 2 | Door 3 | Door 3 | Door 3 | Door 2 | Door 2 |
| Host reveals: | Goat | Goat | Goat | Goat | Goat | Goat |
| Switching: | loses | loses | wins | wins | wins | wins |
This change in the host's behavior causes the car to be twice as likely to be behind the "third door", and is what makes switching to be twice as likely to win in the "host knows" variation of the problem.
Increasing the number of doors
It may be easier to appreciate the solution by considering the same problem with 1,000,000 doors instead of just three (vos Savant 1990). In this case there are 999,999 doors with goats behind them and one door with a prize. The player picks a door. The game host then opens 999,998 of the other doors revealing 999,998 goats—imagine the host starting with the first door and going down a line of 1,000,000 doors, opening each one, skipping over only the player's door and one other door. The host then offers the player the chance to switch to the only other unopened door. On average, in 999,999 out of 1,000,000 times the other door will contain the prize, as 999,999 out of 1,000,000 times the player first picked a door with a goat. A rational player should switch.
Stibel et al. (2008) propose working memory demand is taxed during the Monty Hall problem and that this forces people to "collapse" their choices into two equally probable options. They report that when increasing the number of options to over 7 choices (7 doors) people tend to switch more often, however most still incorrectly judge the probability of success at 50/50.
Combining doors
Instead of one door being opened and shown to be a losing door, an equivalent action is to combine the two unchosen doors into one since the player cannot, and will not, choose the opened door (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008). The player therefore has the choice of either sticking with the original choice of door with a 1/3 chance of winning the car, or choosing the sum of the contents of the two other doors with a 2/3 chance as shown.
The game assumptions play a role here—switching is equivalent to taking the combined contents if and only if the game host knows what is behind the doors, must open a door with a goat, and chooses between two losing doors randomly with equal probabilities.
The only difference between trading for both doors and the trade that is actually offered is whether the host opens one of the two doors. Opening one shows which of these doors the car must be behind if it is behind either. At least one of the two unpicked doors contains a goat, and the host is equally likely to open either of these doors so opening one gives the player no additional information; opening one does not change the 2/3 probability that the car is behind one of them (Devlin 2003).
Simulation
A simple way to demonstrate that a switching strategy really does win two out of three times on the average is to simulate the game with playing cards (Gardner 1959b; vos Savant 1996:8). Three cards from an ordinary deck are used to represent the three doors; one 'special' card such as the Ace of Spades should represent the door with the car, and ordinary cards, such as the two red twos, represent the goat doors.
The simulation, using the following procedure, can be repeated several times to simulate multiple rounds of the game. One card is dealt at random to the 'player', to represent the door the player picks initially. Then, looking at the remaining two cards at least one of which must be a red two, the 'host' discards a red two. If the card remaining in the host's hand is the Ace of Spades, this is recorded as a round where the player would have won by switching; if the host is holding a red two, the round is recorded as one where staying would have won.
By the law of large numbers, this experiment is likely to approximate the probability of winning, and running the experiment over enough rounds should not only verify that the player does win by switching two times out of three, but show why. After one card has been dealt to the player, it is already determined whether switching will win the round for the player; and two times out of three the Ace of Spades is in the host's hand.
If this is not convincing, the simulation can be done with the entire deck, dealing one card to the player and keeping the other 51 (Gardner 1959b; Adams 1990). In this variant the Ace of Spades goes to the host 51 times out of 52, and stays with the host no matter how many non-Ace cards are discarded.
我开始的时候,也认为是 50/50 的机会,所以换不换门,机率都一样。但是看了解释,我就赞同还是要把那个已经打开的门算进来。关键就在你是不是把那个已经打开的门算进来了。直到现在还是有人对这个问题的答案不满意而进行分析研究的。