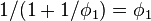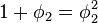除。
黄金比例,又称黄金比,是一种数学上的比例关系。黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。应用时一般取0.618或1.618 ,就像圆周率在应用时取3.14一样。黄金分割早存在于大自然中,呈现于不少动物和植物外观。现今很多工业产品、电子产品、建筑物或艺术品均普遍应用黄金分割,呈现其功能性与美观性。
常用希腊字母  表示黄金比值,用代数式表达就是:
表示黄金比值,用代数式表达就是: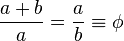
发现
黄金比例是属于数学领域的一个专有名词,但是它最后涵盖的内容不只是有关数学领域的研究,以目前的文献探讨我们可以说黄金比例的发现和如何演进至今仍然是一个谜。但有研究指出公元前6世纪古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,因此现代数学家们推断当时毕达哥拉斯学派已经触及甚至掌握了黄金分割的一些规则,也发现了无理数。他侧重于从数学关系去探讨美的规律,并认为美就是和谐与比例,按照这种比例关系就可以组成美的图案,这其实是一个数字的比例关系,即将一条线分成两部分,较长的一段与较短的一段之比等于全长与较长的一段之比,它们的比例大约是1.618:1。按此种比例关系组成的任何事物都表现出其内部关系的和谐与均衡。
公元前6世纪古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,因此现代数学家们推断当时毕达哥拉斯学派已经触及甚至掌握了黄金分割。 公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,并建立起比例理论。 公元前300年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著。(即中末比)。
中世纪后,黄金分割被披上神秘的外衣,意大利数学家帕乔利称中末比为神圣比例,并专门为此著书立说。德国天文学家开普勒称神圣比例为黄金分割。到19世纪黄金分割这一名称才逐渐通行,而证据在于德国数学家欧姆所写的“基本纯数学”的第二版一书中在注释中写到有关黄金比例的解释,他是这样写 的“人们习惯把按此方式将任一直线分割成两部分的方法,称为黄金分割”而在1875出版的大英百科全书的第九版中,苏利有提到这一段话“由费区那……提出的有趣、实验性浓厚的想法宣称,‘黄金分割’在视觉比例上具有所谓的优越性。”可见黄金分割在当时已经流行了。二十世纪时美国数学家巴尔也给他一个叫phi的名字。黄金分割有许多有趣的性质,人类对它的实际应用也很广泛,造就了他今天的名气。最著名的例子是优选学中的黄金分割法或0.618法,是由美国数学家基弗于1953年首先提出的,70年代在中国推广。
数学解释
两个数值a和b构成黄金比例 ,如果:
,如果: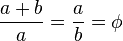
一个得出 数值的方法是从左边的分数式入手。经过简化和代入,
数值的方法是从左边的分数式入手。经过简化和代入,
于是:
两边乘以 就得到:
就得到:
即是
找出该方程的正解,
黄金分割奇妙之处,在于其倒数为自身减1,即:1.618...的倒数为0.618... = 1.618... - 1。
从上面的 得到:
得到:
这个0.618...的数值常用希腊字母 表示,即:
表示,即:
 ,亦可表达为:
,亦可表达为:
例子[编辑]
值
黄金分割数是无理数,前面为:
连分数表示:
平方根表示:
两种表示相等的简单证明:
两边同时乘以 有
有
又
两边同时平方有
因此
黄金分割
黄金分割即  ,其中n为自然数。n=1时为黄金分割((1+√5)/2),n=2时为白银分割(1+√2),n=3时为青铜分割((3+√13)/2)。用连分数表示为
,其中n为自然数。n=1时为黄金分割((1+√5)/2),n=2时为白银分割(1+√2),n=3时为青铜分割((3+√13)/2)。用连分数表示为![n+cfrac{1}{n+cfrac{1}{n+cfrac{1}{n+cfrac{1}{ddots}}}} = [n; n, n, n, n, dots]](http://upload.wikimedia.org/math/e/2/b/e2b0d67e82c0407f896b0f9dec8a7f82.png)


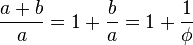
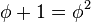










![phi_1 = 1 + cfrac{1}{1 + cfrac{1}{1 + cfrac{1}{1 + cfrac{1}{1 + cfrac{1}{ddots}}}}} = [1;1,1,1,1, ...]](http://upload.wikimedia.org/math/1/e/a/1ea880c76ff64bd8fcac4e0c48f6031f.png)