前两篇文章中,我们讲解了如何利用期权计算器来计算期权价格,如何由期权的市场价格反向计算隐含波动率。读者在学习的过程中,可能已经逐渐意识到期权的交易机会就在计量分析的能力当中。
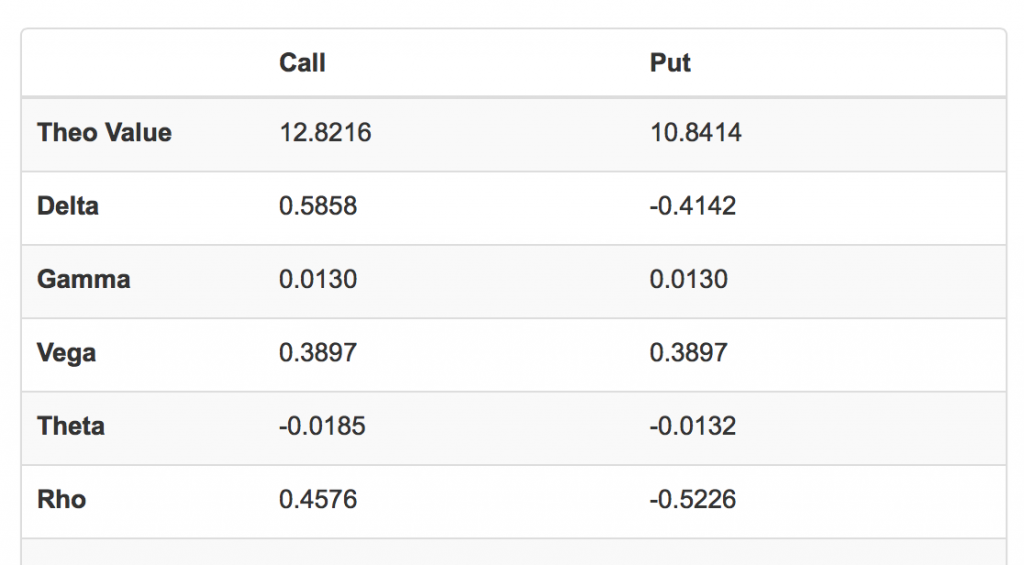
在期权计算器中,我们还有一个重要的功能没有涉及,这就是代表期权不同风险系数的希腊字母。下图就是权翼的期权计算器在默认页面显示的希腊字母输出内容:
还不太熟悉希腊字母的读者,可以阅读这篇短文。
这一节我们介绍什么是Delta, 如何用Delta帮助我们成功的交易。
Delta的定义
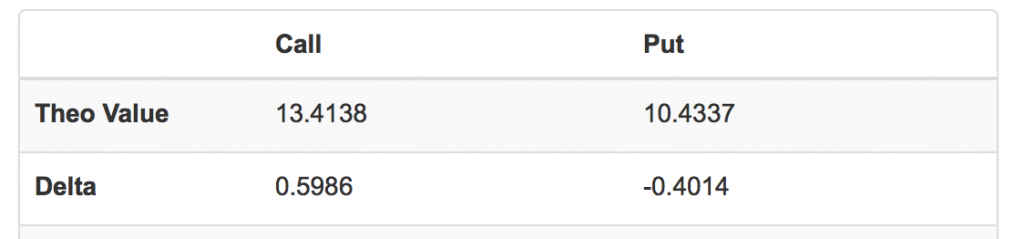
Delta的理论定义为期权价格相对于标的股票价格变化的敏感度。通俗的讲就是当标的股票价格发生微小变化时,期权价格产生的变化。通常我们用两者变化的比率来计量Delta。比如当标的股票价格从$100变化为$101时,看涨期权价格由$12.82变为$13.41,两者变化的比率:(13.41 - 12.82) / (101 - 100) = 0.59或59%,即为该看涨期权在$100股票价格时的Delta。
Delta的特性
Delta不是固定不变的,任何一个期权的Delta会随其它市场变量的变化而变化。比如上面的例子,当股票价格上升到$101时,看涨期权的Delta变为60%,读者可以在期权计算器中模拟。
请读者打开期权计算器,在定价输入框内随意修改定价参数,然后同时观察看涨、看跌期权的Delta变化。细心的读者一定能发现很多特性。例如:
- 看涨期权Delta总是为正,看跌期权Delta总是为负
看涨期权在股票上涨时获利,和股票价格正相关;看跌期权在股票下跌时获利,和股票价格负相关。想明白这一点,这个特性就不言自明了。
- 看涨、看跌期权Delta的绝对值相加为1
读者可能发现,在股息率为零时,不论怎样调整输入变量,看涨、看跌期权Delta的绝对值相加总是为1。这就意味着如果我们买入看涨期权,同时卖出同质的看跌期权,那么组合的Delta为1,也就是我们的简易期权组合可以和标的股票保持同步变化!
这在期权交易中称为合成股票策略(严格讲叫合成期货,细节我们这里不作赘述)。这个策略的优势是我们可以用很小的资金量复制标的股票,为交易提供很高的杠杆。实际操作中,卖出期权需要提交保证金。
感兴趣的读者可以进一步用权益的期货合成策略分析模版,仔细研究策略的构建和不同市场场景下的损益变化。
那么为什么看涨、看跌期权Delta绝对值相加为1呢?或者为什么买入看涨、卖出看跌期权可以合成股票呢?读者还记得我们在期权计算器第一讲中举了平价关系的例子。平价关系的等式为:
c + Ke-rT = p + S0
如果我们调整等号左右两边,可以得到如下新的等式:
c - p = S0 - Ke-rT
等号左边为买入一个看涨期权,同时卖出一个看跌期权;等号右边为标的股票,减去一定量的现金(即行权价的贴现值)。这就是我们上面解释的合成策略。
通过这个例子,读者也更加清楚了平价关系在期权分析中的重要性。它不仅制约了看涨、看跌期权的相对价格,制约了看涨、看跌期权的隐含波动率,而且可以使我们在看涨、看跌期权和股票三者之间互换,之间构建符合我们市场预期的有效交易策略。
- 期权Delta有规律的随股票价格变化
如果读者在练习使用期权计算器时,不断调整股票价格,会发现看涨期权Delta会在0和1之间变动:在其它因素不变时,当股票价格越低(期权为虚值价外期权)时,Delta越低,并接近于0;当股票价格越高(期权为实值价内期权)时,Delta越高,并逐渐接近于1。这意味着虚值的看涨期权对股票价格变化不是非常敏感,而实值期权却非常敏感,深度实值看涨期权(股票价格远远高于行权价的看涨期权),Delta接近为1,基本可以替代标的股票。
对于看跌期权,Delta值在-1和0之间变化,当股票价格越低(期权为实值价内期权)时,Delta越低(但绝对值越高),并逐渐接近于-1;当股票价格越高(期权为虚值价外期权)时,Delta越高(但绝对值越低),并逐渐接近于0。这意味着虚值的看跌期权对股票价格变化不是非常敏感,而实值的看跌期权缺非常敏感,深度实值看跌期权(股票价格远远低于行权价的看跌期权),Delta接近为-1,也就是可以替代做空标的股票。
深度实值看涨、看跌期权的Delta特性,又为投资者提供了一种有效复制标的股票的方法。而这种复制方法,相对于直接买、卖股票,还有很多优势。例如以买入深度看跌期权复制卖空股票的方法,可以以多仓的方式做空,当市场变化与投资者预期方向相反时,投资者最多损失购买期权的期权金,不会像卖空股票一样面临无限风险。
Delta的实用意义
Delta在实际期权分析中,除了计量期权价格相对于股票价格的敏感度,还有更多的实际意义。
- Delta作为对冲的比率
从上面特性分析中,读者会自然想到,假如一个期权合约对应100股标的股票,如果在买入50%Delta的看涨期权的同时,卖出50股标的股票,此时组合就不再受股票价格变化影响了,也就是实现了市场中性。事实的确如此,但这个组合的市场中性只能短暂保持,当股票价格变化幅度稍大,看涨期权的Delta就会偏离50%,整个组合就不再是市场中性了,需要重新买入或卖出一定量的股票来实现平衡。
以标的股票的买、卖来实现期权组合交易的市场中性,是期权市场最重要的手段。我们称这一操作为Delta对冲操作,就是以股票对冲掉期权的Delta风险。
为什么要对冲Delta, 市场中性后怎么盈利?这可能是很多初学者的问题。记得期权风险除Delta之外,还有很多希腊字母代表的风险系数?很多专业期权交易员,认为自己在股票走势的预测上并没有交易优势,那么他们就需要构建市场中性的组合,而将期待的收益集中在有交易优势的风险上。
例如期权做市商有成交时间和成本优势,他们以期权的买、卖差价赚取利润。当做市商从市场买入或卖出期权后,他们需要迅速的以标的股票的交易来对冲掉期权交易的Delta风险,使自己的持仓保持市场中性。
另外,越来越多的期权投资者将波动率的研究作为交易优势。此时他们也需要用Delta中性来规避股票价格风险,而将风险集中在波动率变化上。我们在今后的波动率交易中,会逐步深入的讨论如何培养自己的波动率研究能力,开发自己的交易优势。
期权的Delta会随多个变量而变化,除股票价格外,波动率、时间的推移、股息的变化、市场利率的变化,都会造成Delta的变化。因此,期权交易员要随时监测交易组合的净Delta值,适当时机采取对冲操作。此外,培养自己对Delta变化的大致预估,是初学者迅速培养实战能力的重要方法。读者可以在期权计算器中充分练习,习惯不同市场变量前提下的Delta值。
- 代替标的股票
既然标的股票可以对冲期权,反之,期权也可以代替标的股票。假如我们想买入60股标的股票,除了买入股票现货外,我们还可以买入Delta为60%的看涨期权来替代。同样,假如我们想卖出60股标的股票,除了卖空股票现货外,我们可以买入Delta为-60%的期权。
当然,在用期权替代股票交易时,投资者需要格外谨慎,随时监测期权的Delta变化。
- Delta反应期权到期日时的实值概率
另一个经常为大家忽略,但极为重要的Delta含义是:Delta反应了期权在到期日能够成为实值期权的概率。
我们这里不作具体数学推导。但Delta这一含义为我们学习期权时带来了非常大的实用意义。
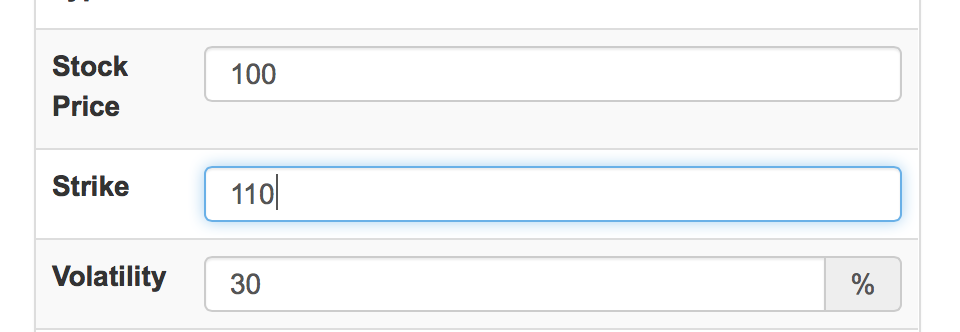
投资者经常会问:今天$100的股票,一年后有多少可能会能涨到$110呢?期权市场为我们提供了市场判断。请读者重新打开期权计算器,在页面默认状态下,修改行权价(Strike)为110:
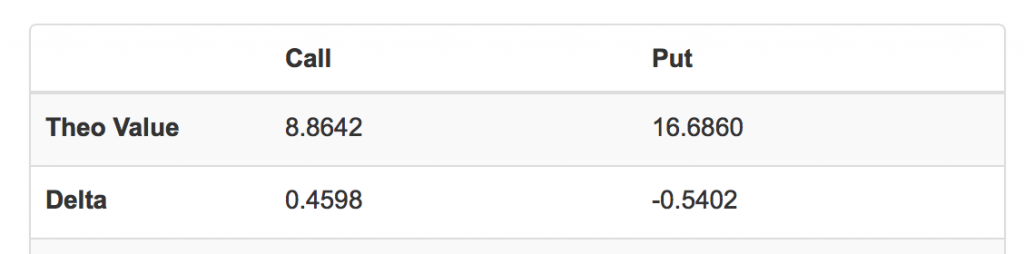
重新计算后,得到以下输出:
我们可以看到,此时一年期、行权价为$110的看涨期权Delta为0.4598。这意味着市场(期权的市场价格)判断该期权在到期日成为实值期权的概率为46%。看涨期权成为实值期权,就是到期日股票价格高于行权价,这就给出了一年时市场价格高于$110的概率。读者要注意,这里的概率是期权市场中的市场价格推算出的概率,也反应的期权交易员对未来标的股票价格变化的预期。
期权分析,就是对标的股票价格未来变化做出的统计分布和概率分析。利用期权的Delta来分析市场对未来价格变化波动的概率,不仅在为我们选择合理的期权时非常重要,而且也为我们揭示了市场对标的股票变化的观点。