做一道题目, 学一个公式, 每一颗子弹消灭一个敌人!
[问题]: A vertex of a Tetrahedron is called trirectangular if all edges of the vertex are perpendicular to each other. Let ABCD be a tetrahedron with A trirectangular. Area [ABC] = 15, [ACD]=16, [ABD]=240. What is the area of [BCD]?
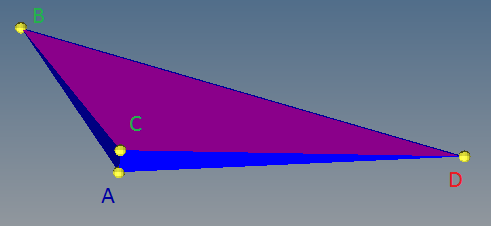
问题来源:http://groups.wenxuecity.com/groups/bbs.php?act=bbsview&gid=1731&basecode=968444
Picture was drawn by ca981.
[学一个公式] 有类似戈股定理的关系:
[BCD]^2 = [ABC] ^2+ [ACD]^2 + [ABD]^2
公式证明 (by student99 http://groups.wenxuecity.com/groups/bbs.php?act=bbsview&gid=1731&basecode=968444)
|
||
| 我想6700417所说的公式可以这样证明: 假设三个面积分别是a, b, c. 那么三个垂直边则分别是:sqrt(2abc)/a, sqrt(2abc)/b, sqrt(2abc)/c. 所以ABCD的体积是sqrt(2abc)/3. 假设A 是原点,三条垂直边分别是x, y, z轴。那么平面BCD 的方程就是:ax + by + cz = sqrt(2abc), 根据点到平面的公式,我们可以求出A 到 BCD 的距离:sqrt(2abc)/sqrt(a^2 + b^2 + c^2) 由此得出:[BCD] * sqrt(2abc)/sqrt(a^2 + b^2 + c^2 ) * 1/3 = sqrt(2abc)/3. 所以 [BCD]^2 = a^2 + b^2 + c^2 . |